Question

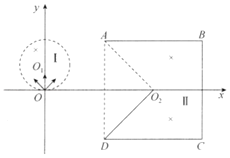
【题目】如图所示，坐标系中，的圆形区域Ⅰ内存在垂直坐标平面向里的匀强磁场，是边长为的正方形，平行于轴，为正方形中心，在围成的区域Ⅱ内也存在垂直坐标平面向里的匀强磁场，为磁场理想边界，两磁场区域磁感应强度均为。、、放置特殊材料，电子接触后被吸收，（不含点）磁场一侧为荧光屏，电子打到荧光屏上被吸收，荧光屏发光。在坐标系第三、四象限存在静止的电子，电子被特殊电场加速后自点沿不同方向、以相同速率进入Ⅰ区域磁场，经过磁场作用所有粒子均垂直边射向Ⅱ区域磁场，电子的质量为，电量为，不考虑二次进入Ⅱ区域的电子，忽略电子间的相互作用和重力。求：

（1）第三、四象限的加速电压的大小；

（2）自点沿轴正方向射入Ⅰ区域的电子，打在荧光屏上位置的纵坐标及该电子在Ⅱ磁场中的运动时间；

（3）荧光屏能发光的长度。

Answer 1

【答案】（1）；（2）-R；；（3）

【解析】

（1）设电子进入磁场速率为，根据动能定理得

电子进入磁场后，由洛伦兹力提供向心力得

解得

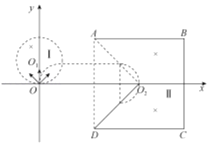
所有粒子均垂直边射向Ⅱ区域磁场，所以由磁场聚焦原理分析得

解得

（2）电子进入Ⅱ区磁场后，轨道半径仍为，轨迹如图所示

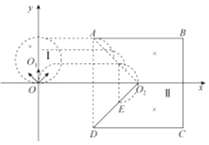
根据对称性，打在荧光屏上点的纵坐标为：

电子在磁场中运动的周期为：

电子的运动时间为：

（3）经分析，沿轴正方向射入Ⅰ区域的电子打在荧光屏的点位置，是电子打到荧光屏的最上端位置，则：

射入Ⅱ区磁场的电子，若轨迹圆心在上，打在点，点为最下端点，根据几何关系：

所以发光长度：