题目内容
如图10所示,一根直杆由粗细相同的两段构成,其中AB段为长x1=5 m的粗糙杆,BC段为长x2=1 m的光滑杆。将杆与水平面成53°角固定在一块弹性挡板上,在杆上套一质量m=0.5 kg、孔径略大于杆直径的圆环。开始时,圆环静止在杆底端A。现用沿杆向上的恒力F拉圆环,当圆环运动到B点时撤去F,圆环刚好能到达顶端C,然后再沿杆下滑。已知圆环与AB段的动摩擦因数μ=0.1,g=10 m/s2,sin 53°=0.8,cos 53°=0.6。试求:
(1)拉力F的大小;
(2)拉力F作用的时间;
(3)若不计圆环与挡板碰撞时的机械能损失,从圆环开始运动到最终静止的过程中在粗糙杆上所通过的总路程。

图10
解析:(1)A→C过程:根据动能定理有
Fx1-mg(x1+x2)sin 53°-μmgx1cos 53°=0-0
恒力
F=![]() =5.1 N
=5.1 N
(2)A→B过程:根据牛顿第二定律和运动学公式有
F-mgsin 53°-μmgcos 53°=ma1
x1=![]() a1t
a1t![]()
解得加速度
a1=![]() =1.6 m/s2
=1.6 m/s2
时间t1= ![]() =2.5 s
=2.5 s
(3)从圆环开始运动到最终静止在粗糙杆上通过的总路程为L,
根据动能定理有Fx1-μmgLcos 53°=0-0
总路程L=![]() =85 m。
=85 m。
答案:(1)5.1 N (2)2.5 s (3)85 m

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
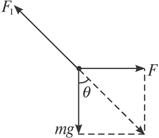
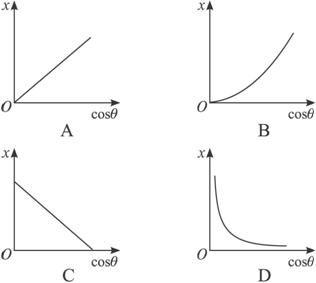
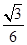 。试求:
。试求: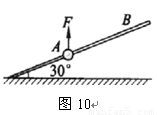
 球B从杆的上端N静止释放,小球B开始运动。(静电力常量
球B从杆的上端N静止释放,小球B开始运动。(静电力常量