��Ŀ����
����Ŀ����ͼ��ʾ��xOy����ϵ�У�y���Ҳ�ռ���ڷ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱ��xOyƽ�����P�������Ϊ����6L��0����Q1��Q2���������ֱ�Ϊ��0��3L������0����3L��������Ϊ����L��0������C��̶�һƽ����y�����һ�㹻���ľ�Ե���Ե��壬���������뵯�Ծ�Ե������ײǰ����y������ٶȲ��䣬��x������ٶȷ���С���䣮���������������Ϊm������Ϊq����������������������������P����PQ1�������ų������ų��˶�����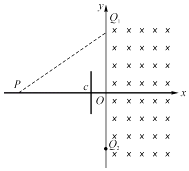
��1��ֻ�뵲����ײһ�β��ܻص�P������ӳ��ٶȴ�С��
��2�������ܷ�����ԭ��O֮���ٻص�P�㣻
��3��ֻ�뵲����ײ���β��ܻص�P������ӳ��ٶȴ�С�Լ���������µ���ij�������Ϊ���٣�
���𰸡�
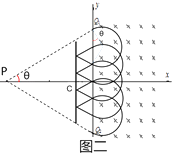
��1���⣺�����뵲��ֻ��ײһ�Σ������˶��Ĺ켣��ͼһ��ʾ�������˶��Ĺ���뾶ΪR����ײǰ�����ų�����֮��ľ���ΪL
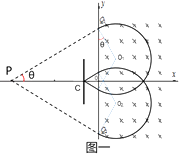
���ݼ��ι�ϵ�ɵã�4Rcos�ȩ�L=6L�����У�cos��= ![]()
��ã�R= ![]() ��
��
���ݰ뾶��ʽ��R= ![]() ��
��
�����٢�ʽ�ɵã�v= ![]()
��ֻ�뵲����ײһ�β��ܻص�P������ӳ��ٶȴ�СΪ ![]() ��
��
��2����������x���Ϸ��뵲����ײn�Σ�
ÿ��Բ���˶�������λ����y������ƽ�Ƶľ���Ϊ2Rcos�ȣ�
�뵲������������λ������ƽ�Ƶľ���ΪL��
һ���������˶�������y�Ṳ����ƽ��Ϊ2Rcos�ȩ�L��
Ҫʹ���Ӿ�������ԭ��O֮���ٻص�P�������㣺
��n��1����2Rcos�ȩ�L��+2Rcos��=3L ��n=2��3��4���� ��
�����ڢ�ʽ�ӿɵã�v= ![]() ��n=2��3��4����
��n=2��3��4����
���ԣ�ֻҪ�����ٶ�����v= ![]() ��n=2��3��4�������ӾͿ��Ծ�������ԭ��O֮���ٻص�P�㣨ͼ��Ϊn=2ʱ�Ĺ���ͼ��
��n=2��3��4�������ӾͿ��Ծ�������ԭ��O֮���ٻص�P�㣨ͼ��Ϊn=2ʱ�Ĺ���ͼ��
�������ܾ�������ԭ��O֮���ٻص�P�㣻
��3�����뵲����ײ���Σ���ͼ����ʾ���赲��ij���L0
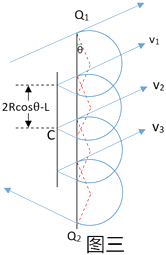
���ݼ��ι�ϵ�ɵã�3��2Rcos�ȩ�L��+2Rcos��=6L
��ã�R= ![]() ��
��
���ݰ뾶��ʽ��R= ![]() �ɵã�v=
�ɵã�v= ![]() ��
��
�����ܢ�ʽ�ӿɵã�����ij��ȵ���СֵL0=2��2Rcos�ȩ�L��=2.5L
��ֻ�뵲����ײ���β��ܻص�P������ӳ��ٶȴ�С�Լ���������µ���ij�������Ϊ2.5L��
����������1�����ȸ�����Ŀ��֪���������˶��Ĺ켣ͼ����������������ǿ�ų����˶���������Ƚ�ϼ��ι�ϵ��������ڴų����˶��Ĺ���뾶�������������ṩ�������ҳ��뾶��ʽ�����ݰ뾶��ʽ������ӵ��ٶȣ�
��2�����ӽ���ų������������˶�����������һ�����ڵ��˶���������ݼ��ι�ϵ�Լ��Գ��ԣ�����������Ӿ�������ԭ��O֮���ٻص�P��������Ĺ�ϵʽ��
��3�������뵲����ײ���β��ܻص�P�㣬�����켣ͼ����ϼ��ι�ϵ�����ð뾶��ʽ������⣮