题目内容
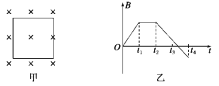
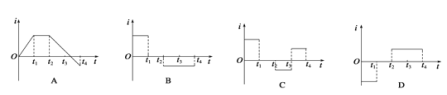
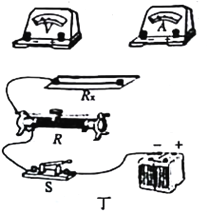
【题目】两位同学用如图所示装置,通过半径相同的A、B两球的碰撞来验证动量守恒定律。
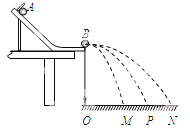
(1)实验中必须满足的条件是 。
A.斜槽轨道尽量光滑以减小误差
B.斜槽轨道末端的切线必须水平
C.入射球A每次必须从轨道的同一位置由静止滚下
D.两球的质量必须相等
(2)测量所得入射球A的质量为mA,被碰撞小球B的质量为mB,图中O点是小球抛出点在水平地面上的垂直投影,实验时,先让入射球A从斜轨上的起始位置由静止释放,找到其平均落点的位置P,测得平抛射程为OP;再将入射球A从斜轨上起始位置由静止释放,与小球B相撞,分别找到球A和球B相撞后的平均落点M、N,测得平抛射程分别为OM和ON。当所测物理量满足表达式 时,即说明两球碰撞中动量守恒;如果满足表达式 时,则说明两球的碰撞为完全弹性碰撞。
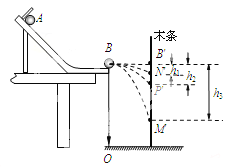
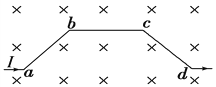
(3)乙同学也用上述两球进行实验,但将实验装置进行了改装:如图12所示,将白纸、复写纸固定在竖直放置的木条上,用来记录实验中球A、球B与木条的撞击点。实验时,首先将木条竖直立在轨道末端右侧并与轨道接触,让入射球A从斜轨上起始位置由静止释放,撞击点为B′;然后将木条平移到图中所示位置,入射球A从斜轨上起始位置由静止释放,确定其撞击点P′;再将入射球A从斜轨上起始位置由静止释放,与球B相撞,确定球A和球B相撞后的撞击点分别为M′和N′。测得B′与N′、P′、M′各点的高度差分别为h1、h2、h3。若所测物理量满足表达式 时,则说明球A和球B碰撞中动量守恒。
【答案】(1)BC;
(2)mA·OP= mA·OM+ mB·ON;OP+OM=ON
(3)![]()
【解析】试题分析:①A、“验证动量守恒定律”的实验中,是通过平抛运动的基本规律求解碰撞前后的速度的,只要离开轨道后做平抛运动,对斜槽是否光滑没有要求,故A错误;
B、要保证每次小球都做平抛运动,则轨道的末端必须水平,故B正确;
C、要保证碰撞前的速度相同,所以入射球每次都要从同一高度由静止滚下,故C正确;
D、为了使小球碰后不被反弹,要求入射小球质量大于被碰小球质量,故D错误;
故选:BC.
②小球离开轨道后做平抛运动,由于小球抛出点的高度相同,它们在空中的运动时间t相等,
它们的水平位移x与其初速度成正比,可以用小球的水平位移代替小球的初速度,
若两球相碰前后的动量守恒,则mAv0=mAv1+mBv2,又OP=v0t,OM=v1t,ON=v2t,代入得:mAOP=mAOM+mBON,
若碰撞是弹性碰撞,则机械能守恒,由机械能守恒定律得:![]() mAv02=
mAv02=![]() mAv12+
mAv12+![]() mBv22,
mBv22,
将OP=v0t,OM=v1t,ON=v2t代入得:mAOP2=mAOM2+mBON2;
③小球做平抛运动,在竖直方向上:h=![]() gt2,平抛运动时间:t=
gt2,平抛运动时间:t=![]() ,
,
设轨道末端到木条的水平位置为x,小球做平抛运动的初速度:
vA=![]() ,vA′=
,vA′=![]() ,vB′=
,vB′=![]() ,
,
如果碰撞过程动量守恒,则:mAvA=mAvA′+mBvB′,
将速度代入动量守恒表达式解得:![]()
故答案为:①BC;②mAOP=mAOM+mBON;mAOP2=mAOM2+mBON2;③![]()