��Ŀ����
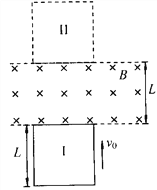
����Ŀ����ͼ��ʾ,һ��ľ������Ϊ![]() ,��Ϊl=6m ,ľ�������Ķ�Ħ������
,��Ϊl=6m ,ľ�������Ķ�Ħ������![]() ,����Ϊ
,����Ϊ![]() ��С���飨���Կ����ʵ㣩����ľ����Ҷ�,С������ľ���Ķ�Ħ������
��С���飨���Կ����ʵ㣩����ľ����Ҷ�,С������ľ���Ķ�Ħ������![]() ����ʼʱľ���뻬�鶼���ھ�ֹ״̬, t=0ʱ��ͻȻ��ľ����ˮƽ���ҵij��ٶ�
����ʼʱľ���뻬�鶼���ھ�ֹ״̬, t=0ʱ��ͻȻ��ľ����ˮƽ���ҵij��ٶ�![]() ʹľ�������˶�, t=2sľ����ǽ�ڷ�����ײ����ľ����ǽ����ײʱ�伫��,��������ԭ���ʵ���,ȡ
ʹľ�������˶�, t=2sľ����ǽ�ڷ�����ײ����ľ����ǽ����ײʱ�伫��,��������ԭ���ʵ���,ȡ![]() ,��:
,��:

��1�� ��ʼʱľ����Ҷ����Ҳ���ֱǽ�ڵľ���L��
��2��С����������ľ����˾��룻
��3�� �����˶�������С������ľ���Ħ��������������
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������(1)ľ���ó��ٶȺ���С���鷢����Ի�����ľ���������ȼ����˶���С�����������ȼ����˶�������ţ�ٵڶ����ɣ����ٶȴ�С�ֱ�Ϊ��
Сľ���ܵ���Ħ������fm=��1mg=0.4��2��10=8N
ľ���ܵ������Ħ������fM=��1(m+M)g=0.2��(2+4)��10=12N��
am=fm/m=��1g=4m/s2
aM=��fm+f����/M=(8+12)/4=5m/s2
��ľ����ǽ��ײʱ�����ߵ��ٶ�������ȣ��蹲ͬ���ٶ�Ϊv����
amt=v0aMt=v
�������ݵã�t=1s��v=4m/s
�ù�����ľ���λ�ƣ�x1=v0t![]() =6.5m��
=6.5m��
���ߵ��ٶ���Ⱥ�����������ȵļ��ٶ��˶�����
a=![]() <am
<am
�ɷ�����֪�����߿�������ȵļ��ٶ�һ����١��پ�1s�����ٵ�λ�ƣ�
x2= ![]()
��ʼʱľ����Ҷ����Ҳ���ֱǽ�ڵľ���L=x1+x2=9.5m
��2���������ǽ����ײʱ���ٶ�Ϊv1���ɹ�ʽ��2ax2=![]()
�������ݵã�v1=2m/s
��ľ�巴����ľ�������˶�����Сľ�������������˶�����������֪�����ߵļ��ٶȵĴ�С�뿪ʼʱ�ļ��ٶȵĴ�С����ȵģ�
��ľ�徭��ʱ��t�����ٶȱ��0,��v1aMt��=0
���ԣ�t��=0.4s
��ʱС������ٶȣ�v2=v1amt��=24��0.4=0.4m/s��
�˺�����Сľ����ľ��֮���Ħ����С��ľ�������֮������Ħ��������������һ��ʱ����ľ�屣�ֲ��������������ľ���ϼ��٣�ֱ��ֹͣ��
ľ����ľ����ٶ����ǰ,Сľ���λ�ƣ�x2= ![]()
Сľ�鵽ľ����Ҷ˵ľ��룺��x1=x1x2=6.52=4.5m
ľ�巴�����ľ�������λ�ƣ�x3= ![]()
Сľ�����λ�ƣ�x4= ![]()
С����ֹͣʱ��ľ���Ҷ˵ľ��룺S=��x1-��x2=4.5-0.4-0.5=3.6m��
С����������ľ����˾���Ϊ![]() L-S=6m-3.6m=2.4m
L-S=6m-3.6m=2.4m
��3��ľ����ľ����ٶ����ǰ��С������ľ���Ħ������������![]()
ľ�巴�����С������ľ���Ħ������������![]()
�����˶�������С������ľ���Ħ������������Q=Q1+Q2=36J+7.2J=43.2J

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�