题目内容
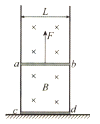
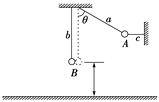
【题目】质量为m的A球和质量为3m的B球分别用长为L的细线a和b悬挂在天花板下方,两球恰好相互接触,用细线c水平拉起A,使细线a偏离竖直方向θ=60°,静止在如图所示的位置。细线b能承受的最大拉力Fm=4.5mg,重力加速度为g,剪断细线c,问:
(1)A与B发生碰撞前瞬间A的速度大小。
(2)若A与B发生的是弹性碰撞,求碰撞后瞬间B的速度大小。
(3)请你判断细线b是否会被拉断。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)细线b不会被拉断。
;(3)细线b不会被拉断。
【解析】(1)A球受力如图所示,根据物体的平衡条件有:Ta=![]() =
=![]() =2mg
=2mg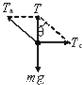
A与B发生碰撞前瞬间的速度大小为v,由机械能守恒定律有:
mgL(1-cosθ)=![]()
解得,v=![]()
(2)A与B发生弹性碰撞,则由动量守恒和动能守恒得:
mv=mvA+3mvB
![]() =
=![]() +
+![]()
解得,vB=![]()
(3)假设b不断,绳子的拉力大小为F,则根据牛顿第二定律:
F-3mg=3m![]()
解得:F=3.75mg<Fm=4.5mg,故b不会被拉断

练习册系列答案
相关题目