题目内容
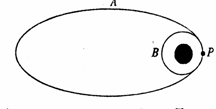
我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行（即绕地球一圈需要24小时）；然后，经过两次变轨依次到达“48小时轨道”和“72小时轨道”；最后奔向月球．如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨完成后与变轨前相比，（ ）
分析：卫星在各自轨道上做圆周运动向心力由万有引力提供，讨论轨道半径与周期的关系，根据周期确定轨道半径大小，再根据半径确定角速度、线速度、引力的大小变化情况．
解答：解：万有引力提供向心力有：G
=mr
可得运动半径与周期的关系为：r=
，由题意可得：r24＜r48＜r72
A、根据万有引力提供向心力有：G
=mrω2得ω=
，随着r增大，万有引力减小，角速度减小，故A正确；
B、根据万有引力提供向心力有：G
=mrω2得ω=
，随着r增大，万有引力减小，角速度减小，故B错误；
C、根据万有引力提供向心力有：G
=m
得v=
，随着 r增大，线速度v关小，卫星动能减小，由于卫星轨道增加的过程中克服引力做功，故势能增大，故C错误；
D、根据万有引力提供向心力有：G
=m
得v=
，随着 r增大，线速度v关小，卫星动能减小，由于卫星轨道增加的过程中克服引力做功，故势能增大，故D正确．
故选AD．
| mM |
| r2 |
| 4π2 |
| T2 |
| 3 |
| ||
A、根据万有引力提供向心力有：G
| mM |
| r2 |
|
B、根据万有引力提供向心力有：G
| mM |
| r2 |
|
C、根据万有引力提供向心力有：G
| mM |
| r2 |
| v2 |
| r |
|
D、根据万有引力提供向心力有：G
| mM |
| r2 |
| v2 |
| r |
|
故选AD．
点评：万有引力提供圆周运动向心力，讨论半径与线速度、周期、及角速度的关系，知道克服引力做功卫星的引力势能增加．
练习册系列答案
相关题目
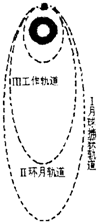2007年10月24日18时零5分，我国成功发射一颗探月卫星“嫦娥一号”．探月卫星绕地经过3次变轨飞行180多万公里，于2007年11月5日成功进入月球捕获轨道，如图I轨道；11月6日经第2次变轨进入环月轨道，如图II轨道；11月7日经第3次变轨进入工作轨道，如图9-III轨道．经过测试调整于2007年11月20日向地球发回首张照片，“嫦娥一号”成功发射在我国又掀起了新一轮航天热．关于“嫦娥一号”探月卫星，下列说法正确的是（ ）
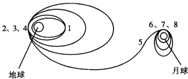2007年10月24日18时，我国成功发射了“嫦娥一号”探月卫星，卫星经过八次点火变轨后，绕月球做匀速圆周运动．图中所示为探月卫星运行轨迹的示意图（图中1、2、3、4、…、8为卫星运行中的八次点火位置），则下述说法正确的是（ ）我国“嫦娥一号”探月卫星发射后，先在“24小时轨道”上绕地球运行（即绕地球一圈需要24小时）；然后，经过两次变轨依次到达“48小时轨道”和“72小时轨道”；最后奔向月球．如果按圆形轨道计算，并忽略卫星质量的变化，则在每次变轨完成后与变轨前相比，（ ）
| A、卫星绕行速度变大 | B、卫星所受向心力增大 | C、卫星的机械能守恒 | D、卫星动能减小，引力势能增大 |
=
