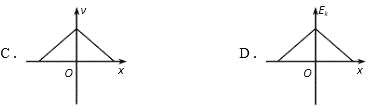题目内容
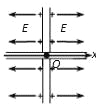
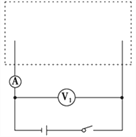
【题目】如图所示,间距为L=![]() 、长为5.0m的光滑导轨固定在水平面上,一电容为C=0.1F的平行板电容器接在导轨的左端。垂直于水平面的磁场沿x轴方向上按
、长为5.0m的光滑导轨固定在水平面上,一电容为C=0.1F的平行板电容器接在导轨的左端。垂直于水平面的磁场沿x轴方向上按![]() (其中
(其中![]() ,
,![]() )分布,垂直x轴方向的磁场均匀分布。现有一导体棒横跨在导体框上,在沿x轴方向的水平拉力F作用下,以v=
)分布,垂直x轴方向的磁场均匀分布。现有一导体棒横跨在导体框上,在沿x轴方向的水平拉力F作用下,以v=![]() 的速度从
的速度从![]() 处沿x轴方向匀速运动,不计所有电阻,下面说法中正确的是
处沿x轴方向匀速运动,不计所有电阻,下面说法中正确的是

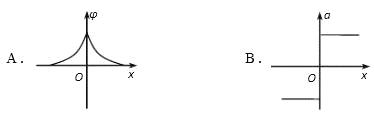
A. 电容器中的电场随时间均匀增大
B. 电路中的电流随时间均匀增大
C. 拉力F的功率随时间均匀增大
D. 导体棒运动至![]() m处时,所受安培力为0.02N
m处时,所受安培力为0.02N
【答案】AC
【解析】根据导体切割磁感应线产生的感应电动势计算公式可得E=BLv,所以△E=△BLv,由于磁场随位移均匀变化,所以感应电动势随位移均匀增大,电容器两端的电压均匀变化,电场强度也是均匀变化的,A正确;电容器的电容![]() ,解得:I=
,解得:I=![]() LCv,由于导体棒匀速运动,且磁感应强度随位移均匀变化,而x=v△t,所以电流强度不变,B错误;
LCv,由于导体棒匀速运动,且磁感应强度随位移均匀变化,而x=v△t,所以电流强度不变,B错误;
导体棒匀速运动,根据平衡条件可得F=BIL,而B均匀增大,所以安培力均匀增大,拉力F均匀增大,拉力做功功率等于克服安培力做功功率,即P=Fv可知,外力的功率均匀增大,C正确;导体棒运动至x=3m处时,磁感应强度为B=(0.4+0.2×3)T=1T,电流强度:I=![]() LCv=
LCv=![]() LCv2=0.2×1×0.1×4A=0.08A,所以导体棒所受安培力为FA=BIL=1×0.08×1N=0.08N,故D错误.故选AC.
LCv2=0.2×1×0.1×4A=0.08A,所以导体棒所受安培力为FA=BIL=1×0.08×1N=0.08N,故D错误.故选AC.

练习册系列答案
相关题目