题目内容
4. 如图所示,在足够长的光滑水平地面上静置一质量为M的小球B,质量为m的弹性小球自光滑曲面的某一高度由静止开始自由下滑,在水平面上与B球发生不计机械能损失的正碰,若M=9m,问小球至多能碰几次?
如图所示,在足够长的光滑水平地面上静置一质量为M的小球B,质量为m的弹性小球自光滑曲面的某一高度由静止开始自由下滑,在水平面上与B球发生不计机械能损失的正碰,若M=9m,问小球至多能碰几次?
分析 小球碰撞过程动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律求出碰撞后两球的速度;当后面球的速度大于前面球的速度时,两球能发生碰撞,根据两球的速度关系判断两球碰撞的次数.
解答 解:设小球m从高为h处下滑,下滑过程机械能守恒,
由机械能守恒定律得:mgh=$\frac{1}{2}$mv02,解得:v0=$\sqrt{2gh}$,
m、M碰撞过程系统动量守恒,以向右为正方向,
由动量守恒定律得:mv0=mv1+MvB1
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$MvB12,
已知:M=9m,解得:v1=-$\frac{4}{5}$$\sqrt{2gh}$,负号表示方向向左,vB1=$\frac{1}{5}$$\sqrt{2gh}$,
m小球碰撞后反向运动,冲上曲面,然后再下滑,返回水平面时的速度为:v1′=v1=$\frac{4}{5}$$\sqrt{2gh}$,
小球与B发生第二次碰撞过程,以向右为正方向:
由动量守恒得:mv1′+MvB1=mv2+MvB2,
由机械能守恒定律得:$\frac{1}{2}$mv1′2+$\frac{1}{2}$MvB12=$\frac{1}{2}$mv22+$\frac{1}{2}$MvB22=$\frac{1}{2}$mv02,
解得:v2=-$\frac{7}{25}$$\sqrt{2gh}$,负号表示方向随便向左,vB2=$\frac{8}{25}$$\sqrt{2gh}$,
m小球与B发生第二次碰撞后反向运动,冲上曲面,然后再下滑,
返回水平面时的速度为:v2′=v2=$\frac{7}{25}$$\sqrt{2gh}$<vB2=$\frac{8}{25}$$\sqrt{2gh}$,
两球不能再次发生碰撞,所以两球最多能碰撞两次.
答:小球至多能碰2次.
点评 本题考查了求两球碰撞的次数问题,对于弹性碰撞,动量守恒和机械能守恒是基本规律,知道两球发生碰撞的条件、应用动量守恒定律与机械能守恒定律即可正确解题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 用如图a所示的圆弧斜面装置研究平抛运动,每次将质量为m的小球从半径为R的四分之一圆弧形轨道不同位置静止释放,并在弧形轨道最低点水平部分处装有压力传感器测出小球对轨道压力的大小F.已知斜面与水平地面之间的夹角θ=30°,实验时获得小球在斜面上的不同下落高度h,最后作出了如图b所示的F-h图象,g取10m/s2,则由图可求得圆弧轨道的半径R为( )
用如图a所示的圆弧斜面装置研究平抛运动,每次将质量为m的小球从半径为R的四分之一圆弧形轨道不同位置静止释放,并在弧形轨道最低点水平部分处装有压力传感器测出小球对轨道压力的大小F.已知斜面与水平地面之间的夹角θ=30°,实验时获得小球在斜面上的不同下落高度h,最后作出了如图b所示的F-h图象,g取10m/s2,则由图可求得圆弧轨道的半径R为( )| A. | 0.125 m | B. | 0.25 m | C. | 0.50 m | D. | 0.75 m |
 如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )
如图所示,细线a,b,c的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°、60°和45°,如果三根细线都处于伸直状态,设a,b,c受到的拉力分别为Ta,Tb和Tc,氢气球受到的浮力为F,则( )| A. | 细线受到的拉力中Ta一定最大 | |
| B. | 三根细线的拉力都不为零时,有可能Ta=Tb=Tc | |
| C. | 三根细线的拉力的竖直分量之和一定等于F | |
| D. | 三根细线的拉力的竖直分量之和一定小于F |
 如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )
如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )| A. | x可能是电感线圈,y可能是电容器 | B. | x可能是电容器,y可能是电感线圈 | ||
| C. | x可能是二极管,y可能是电容器 | D. | x可能是电感线圈,y可能是二极管 |
| A. | 物体在5s时指的是物体在5s末这一时刻 | |
| B. | 物体在5s内指的是物体在4s末到5s末这1s的时间 | |
| C. | 物体在第5s内指的是物体在4s末到5s末这1s的时间 | |
| D. | 第4s末就是第5s初,指的是时刻 |
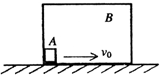 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为$\frac{M}{5}$可视为质点的物体A,A与B、B与地面间的动摩因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离S(S<L)后也停止运动.矩形盒B运动的总时间是( )| A. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{6μg}$ | B. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{5μg}$ | ||
| C. | t=$\frac{{\sqrt{v_0^2-2μgL}-\sqrt{2μgS}}}{7μg}$ | D. | t=$\frac{{5(\sqrt{v_0^2-2μgL}-\sqrt{2μgS})}}{7μg}$ |
 一定量的理想气体经历了如图所示的abca一个循环过程,其中a→b过程气体体积减小(填“增大”、“减小”或“不变”),若c→a过程气体放出热量10J,则气体经历a→b→c过程内能的变化是10J.
一定量的理想气体经历了如图所示的abca一个循环过程,其中a→b过程气体体积减小(填“增大”、“减小”或“不变”),若c→a过程气体放出热量10J,则气体经历a→b→c过程内能的变化是10J. 用如图所示的装置测量物块A与水平桌面间的动摩擦因数.将物块A置于水平桌面上,用轻绳绕过轻质定滑轮与物块B相连,不计绳子质量、不计绳与滑轮间的摩擦力、不计空气阻力.实验时将连接A的细绳调节至与桌面平行,按压住物块A使B物块自然悬垂,系统稳定后用米尺测出此时物块B距离地面的高度h,然后由静止释放A,B物块拉动A运动,B落地后即可停止,物块A继续在桌面上滑行一段距离后停在桌面上.为测出物块A与水平桌面间的动摩擦因数,本实验还需要测量的物理量是A、B的质量,滑块A运动的总距离,除米尺外还需要的测量仪器是天平,所测动摩擦因数的表达式为 μ=$\frac{{m}_{B}h}{({m}_{A}+{m}_{B})s+{m}_{B}h}$,式中各符号的意义是mA、mB分别为A、B的质量,s为滑块A运动的总距离.
用如图所示的装置测量物块A与水平桌面间的动摩擦因数.将物块A置于水平桌面上,用轻绳绕过轻质定滑轮与物块B相连,不计绳子质量、不计绳与滑轮间的摩擦力、不计空气阻力.实验时将连接A的细绳调节至与桌面平行,按压住物块A使B物块自然悬垂,系统稳定后用米尺测出此时物块B距离地面的高度h,然后由静止释放A,B物块拉动A运动,B落地后即可停止,物块A继续在桌面上滑行一段距离后停在桌面上.为测出物块A与水平桌面间的动摩擦因数,本实验还需要测量的物理量是A、B的质量,滑块A运动的总距离,除米尺外还需要的测量仪器是天平,所测动摩擦因数的表达式为 μ=$\frac{{m}_{B}h}{({m}_{A}+{m}_{B})s+{m}_{B}h}$,式中各符号的意义是mA、mB分别为A、B的质量,s为滑块A运动的总距离.