Question

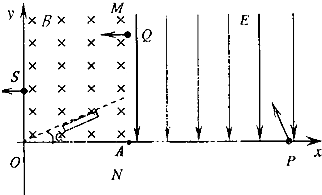（2011?唐山二模）如图在平面直角坐标系xOy第一象限内有一竖直挡板MN，挡板左侧存在着垂直于纸面向里的匀强磁场，右侧存在竖直向下的匀强电场．在磁场中放置一小绝缘板，其上表面过原点O且与x轴成α角，x轴上的P点处有一粒子源向各个方向发射速度大小相等的带电粒子．其中一粒子沿水平方向穿过挡板MN上的小孔Q进入磁场，在磁场中偏转后垂直撞到绝缘板上，与绝缘板发生没有能量损失的碰撞，之后从磁场边界上S点沿平行于x轴的方向射出匀强磁场．若已知AP=4L，AQ=2L，电场强度为E，带电粒子的电荷量为q，质量为m，α角等于30°不计粒子的重力．求：
（1）该粒子从粒子源发射的速度大小为多少？
（2）磁场的磁感应强度B为多少？
（3）粒子从P点到S点所用的时间为多少？

Answer 1

分析：（1）粒子从P点发出后做斜上抛运动，水平方向做匀速直线运动，竖直方向做匀减速直线运动，到达G时末速度为零．根据牛顿第二定律和运动学公式结合分析研究水平和竖直两个方向的位移，即可求出从粒子源发射的速度大小．
（2）粒子在磁场中由洛伦兹提供向心力而做匀速圆周运动，画出轨迹，由几何知识可求出半径，由牛顿第二定律可求得B．
（3）求出粒子磁场中的运动时间，再求出总时间．先求出周期，再由t=

θ

2π

T，根据圆心角θ求出磁场中运动时间．

解答：解：（1）设通过小孔Q的粒子在P点沿x轴方向的速度为v_x，y轴方向的速度为v_y，在电场中运动的时间为t₁．该粒子从P点发出后做斜上抛运动，水平方向做匀速直线运动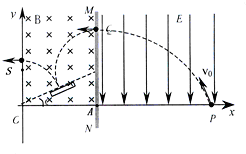，竖直方向做匀减速直线运动，到达G时末速度为零．则
  x轴方向：4L=v_xt₁
  y轴方向：2L=

1

2

?

qE

m

t

2 1

，v_y=

qE

m

t1
解得，t₁=2

mL qE

      v_x=v_y=2

qEL m

故该粒子从粒子源发射的速度大小为 v0=2

2qEL m

．
（2）粒子在磁场中由洛伦兹提供向心力而做匀速圆周运动，画出轨迹如图，由几何知识得
其运动半径为  R=L
由qv_xB=m

v 2 x

R

，得 B=2

mE qL

（3）粒子在磁场运动的周期为T=

2πm

qB

，其轨迹所对应的圆心角为θ=120°+60°=180°
则在粒子在磁场运动的时间为t₂=

1

2

T=

πm

qB

=

π

2

mL qE

故粒子从P点到S点所用的时间为
   t=t₁+t₂=2

mL qE

+

π

2

mL qE

．
答：
（1）该粒子从粒子源发射的速度大小为2

2qEL m

；
（2）磁场的磁感应强度B为2

mE qL

；
（3）粒子从P点到S点所用的时间为2

mL qE

+

π

2

mL qE

．

点评：此类型的题首先要对物体的运动进行分段，然后对物体在各段中进行正确的受力分析和运动的分析，进行列式求解．粒子在磁场运动时间的确定：利用圆心角与弦切角的关系或者四边形的内角和等于360°计算出粒子所经过的圆心角θ的大小，用公式t=

θ

2π

T可求出运动时间．