题目内容
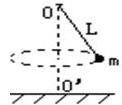
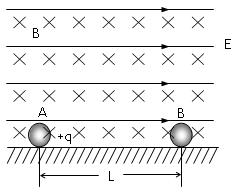
(08年韶关市模拟)(18分)在光滑绝缘的水平面上方,有一足够大的空间,此空间同时存在电场强度为E、方向水平向右的匀强电场和磁感应强度为B、方向垂直纸面向里的匀强磁场.在水平面上沿电场线方向放有两个静止的小球A和B(均可看成质点),两小球的质量均为m ,A球带电荷量+q ,B球不带电,开始时两球相距L.现释放两球,A球开始运动,当A、B碰撞时(碰撞时间可忽略),A、B两球的总动能无损失,且A、B两球间无电荷转移.不考虑空气阻力,求:
(1)如果 A球与B球能够发生碰撞,从释放两球至两球发生第一次碰撞需要多长时间?第一次碰撞后A、B两球的速度各为多大?
(2)设q=2×10-5C,E=1×104N/C,m=0.1kg,B=50T,L=1cm,取g=10m/s2,各次碰撞时相邻两次碰撞的时间间隔分别是多少?A、B两球最多能相碰几次?
解析:
(1)当两球能够发生第一次碰撞时,A球没有离开水平面,沿水平方向只受电场力的作用,做匀加速直线运动,且满足
![]() (1分)
(1分)
![]() (1分)
(1分)
联立以上各式得:![]() (1分)
(1分)
![]() (1分)
(1分)
即经过时间![]() 两球发生第一次碰撞.
两球发生第一次碰撞.
A球与B球第一次碰撞时,动量守恒,则![]() (1分)
(1分)
根据题意,总能量不损失,则![]() (1分)
(1分)
联立解得![]() (2分)
(2分)
(2)设![]()
代入数值求得![]() o=0.2m/s to=0.1s a=2m/s2 (1分)
o=0.2m/s to=0.1s a=2m/s2 (1分)
设每次碰撞前,A、B的速度分别为![]() 1、
1、![]() 2 ,碰撞后分别为
2 ,碰撞后分别为![]() 、
、![]() ,由于碰撞中动量守恒,总动能不损失,所以:
,由于碰撞中动量守恒,总动能不损失,所以:
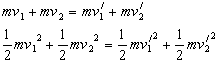
解得 ![]()
![]() (2分)
(2分)
即碰撞后两球总是交换速度.
由上一问可知,第一次碰后A球速度为0 ,此后作匀加速直线运动;B球作速度为![]() 0 的匀速直线运动.
0 的匀速直线运动.
设第二次碰撞前A球速度为vA2 ,所用时间为△t2 ,则
![]()
![]()
解得![]()
![]() (2分)
(2分)
碰撞后,交换速度,A的速度变为v0 ,B的速度变为2v0
设第三次碰撞前A球速度为vA3,所用时间为△t3 ,,则
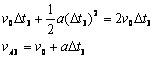
解得![]() A3=3
A3=3![]() 0
0 ![]() (1分)
(1分)
再次碰撞后,交换速度,A的速度变为2![]() 0 ,B的速度变为3
0 ,B的速度变为3![]() 0
0
同理可证,第一次碰撞后的过程中,A、B每次碰撞前的加速过程(即相邻两次碰撞的间隔),时间均相等,为
2t=0.2s (1分)
同时可得,A球加速n次后的速度为n![]() 0 .碰后速度为(n-1)
0 .碰后速度为(n-1)![]() 0.每一次碰后至下一次碰前速度增加2
0.每一次碰后至下一次碰前速度增加2![]() 0
0
设加速n次后A球刚要离开地面,则
nq![]() 0B=mg (2分)
0B=mg (2分)
代值解得 n=5×103 即最多碰5000次. (1分)