Question

【题目】有一条沿顺时针方向匀速传送的传送带，恒定速度v＝4 m/s，传送带与水平面的夹角θ＝37°，现将质量m=1kg的小物块轻放在其底端（小物块可视作质点），与此同时，给小物块沿传送带方向向上的恒力F＝8N，经过一段时间，小物块上到了离地面高为＝2．4 m的平台上。已知物块与传送带之间的动摩擦因数μ＝0．5，（g取10 m/s2， sin37°＝0．6，cos37°＝0．8）．问：

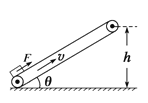
（1）物块从传送带底端运动到平台上所用的时间？

（2）若在物块与传送带达到相同速度时，立即撤去恒力F，计算小物块还需经过多少时间离开传送带以及离开时的速度？

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）对物块受力分析可知，物块先是在恒力作用下沿传送带方向向上做初速为零的匀加速运动，直至速度达到传送带的速度，由牛顿第二定律：

，

计算得：

加速时间：，加速距离：

物块达到与传送带同速后，对物块受力分析发现，物块受的摩擦力的方向改向，

因为而下滑力和最大摩擦力之和为。故不能相对斜面向上加速。

故得：

匀速运动时间：

到平台所用的时间：

（2）若达到同速后撤力F，对物块受力分析，因为，

故减速上行，得

物块还需离开传送带，离开时的速度为，则

，，