题目内容
6. 如图所示,在平面直角坐标系xoy中,第一象限存在沿y轴负方向的匀强电场,第四象限存在垂直纸面向外的匀强磁场,磁感应强度B=$\frac{m{v}_{0}}{qL}$.一质量为m、电荷量为q的带正电粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上N点与x轴正方向成θ=60°角射入匀强磁场中,最后从y轴负半轴某一点P射出,已知M点坐标为(0,3L),不计粒子重力,求:
如图所示,在平面直角坐标系xoy中,第一象限存在沿y轴负方向的匀强电场,第四象限存在垂直纸面向外的匀强磁场,磁感应强度B=$\frac{m{v}_{0}}{qL}$.一质量为m、电荷量为q的带正电粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上N点与x轴正方向成θ=60°角射入匀强磁场中,最后从y轴负半轴某一点P射出,已知M点坐标为(0,3L),不计粒子重力,求:(1)匀强电场的电场强度和粒子到N点的速度;
(2)粒子在磁场中运动的轨道半径和粒子打在P点的坐标;
(3)粒子从进入M点运动到P点所用的总时间.
分析 (1)粒子在电场中运动时做类平抛运动,水平方向匀速直线运动,竖直方向做初速度为零的匀加速直线运动,可以解出电场强度与粒子的速度;
(2)根据洛伦兹力提供向心力解出粒子做圆周运动的半径,结合几何关系解出粒子打到y轴的位置.
(3)根据粒子在磁场中的运动轨迹可以求得粒子做类平抛运动在x轴方向的位移,由于在x轴方向做匀速直线运动,故类平抛时间t可求.根据轨迹的圆心角可由t=$\frac{θ}{2π}•T$求出粒子在磁场中运动的时间,即可得到总时间.
解答 解:(1)粒子在电场中运动时做类平抛运动:水平方向匀速直线,竖直方向做初速度为零的匀加速直线运动,合速度与分速度的关系如图:
$tan60°=\frac{{v}_{y}}{{v}_{x}}$
则:${v}_{y}=\sqrt{3}{v}_{0}$
${v}_{y}=at=\frac{qEt}{m}=\sqrt{3}{v}_{0}$…①
且竖直方向做初速度为零的匀加速直线运动:OM=$\frac{1}{2}$at2=$\frac{qE}{2m}{t^2}=3L$…②
由①②解得:$E=\frac{mv_0^2}{2qL}$
${v_N}=\sqrt{v_x^2+v_y^2}=2{v_0}$
(2)粒子在电场中运动,竖直方向的平均速度:$\overline{{v}_{y}}$=$\frac{0+{v}_{y}}{2}$=$\frac{\sqrt{3}}{2}{v}_{0}$,
所以竖直方向的位移:3L=$\frac{\sqrt{3}}{2}{v}_{0}t$…③
水平方向的位移:x=0N=v0t…④
由③④解得:x=2$\sqrt{3}$L
由洛伦兹力提供向心力得:$qB{v_N}=m\frac{{{v_N}^2}}{R}$
则$R=\frac{{m{v_N}}}{qB}=2L$
粒子在磁场中的运动轨迹如图:
由图可以看出PN与x轴方向的30°,由于ON等于2$\sqrt{3}$L,
则:PN=$\frac{ON}{cos30°}$=4L
PN距离恰好为半径的两倍,说明粒子正好从NP直径出第四象限
即打在y 轴负半轴的坐标(0,-2L)
(3)粒子在电场中做类平抛运动,水平位移x=0N=v0t=2$\sqrt{3}$L,
解得:t=$\frac{2\sqrt{3}L}{{v}_{0}}$
粒子在磁场中运动轨迹为半圆,所需的时间:t2=$\frac{πR}{{v}_{N}}$=$\frac{π2L}{2{v}_{0}}$=$\frac{πL}{{v}_{0}}$
所以粒子的运动总时间为t总=$\frac{{2\sqrt{3}L+πL}}{v_0}$
答:(1)匀强电场的电场强度为$\frac{m{v}_{0}^{2}}{2qL}$,粒子到N点的速度为2v0;
(2)粒子在磁场中运动的轨道半径为2L,粒子打在P点的坐标为(0,-2L);
(3)粒子从进入M点运动到P点所用的总时间为$\frac{{2\sqrt{3}L+πL}}{v_0}$.
点评 本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握圆周运动及平抛运动的基本公式,难度适中.

 单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )
单匝矩形线圈在匀强磁场中匀速转动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则( )| A. | 线圈中O时刻感应电动势最大 | |
| B. | 线圈中D时刻感应电动势为零 | |
| C. | 线圈中D时刻感应电动势最大 | |
| D. | 线圈中O至D时间内平均感电动势为0.4V |
| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不能确定 |

| A. | 在t=0时,质点位移为零,速度和加速度也为零 | |
| B. | 在t=4s时,质点的速度最大,方向沿y轴的负方向 | |
| C. | 在t=3s时,质点振幅为-5cm,周期为4s | |
| D. | 无论何时,质点的振幅都是5cm,周期都是4s |
 如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )
如图,一束光沿半径方向射向一块半圆形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线,则( )| A. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| B. | 在真空中,a光的波长小于b光的波长 | |
| C. | 若改变光束的入射方向使θ角逐渐变大,则折射光线b首先消失 | |
| D. | 分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |
 如图所示,理想变压器的原线圈接在u=220$\sqrt{2}$sin(100πt)V的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表,下列说法正确的是( )
如图所示,理想变压器的原线圈接在u=220$\sqrt{2}$sin(100πt)V的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表,下列说法正确的是( )| A. | 原线圈中电流表的读数为$\sqrt{2}$A | |
| B. | 原线圈中的输入功率为220W | |
| C. | 副线圈中电压表的读数为110V | |
| D. | 副线圈中输出交变电流的周期为50s |
 如图所示,两个相通的容器 P、Q间装有阀门K,P中充满气体,气体分子间的相互作用力可以忽略,Q中为真空,整个系统与外界没有热交换,打开阀门K后,P中的气体进入Q中,最终达到平衡状态,则( )
如图所示,两个相通的容器 P、Q间装有阀门K,P中充满气体,气体分子间的相互作用力可以忽略,Q中为真空,整个系统与外界没有热交换,打开阀门K后,P中的气体进入Q中,最终达到平衡状态,则( )| A. | 气体体积膨胀,对外做功,内能减小 | |
| B. | 气体体积膨胀,温度降低,压强减小 | |
| C. | 分子的平均动能不变,但分子的密度减小了,所以气体压强也要减小 | |
| D. | Q中的气体能自发地全部退回到P中 |
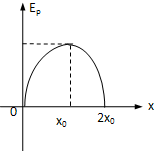
 如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )
如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )