题目内容
11.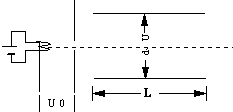 如图所示,在炽热的金属丝和金属板间加上电压U0=2500V,从炽热的金属丝射出的电子在真空中被加速后,从金属板的小孔水平穿出,接着射入水平放置的两平行金属板间.已知两板的长度L=6.0cm,相距d=2cm,板间电压U=200V.求:
如图所示,在炽热的金属丝和金属板间加上电压U0=2500V,从炽热的金属丝射出的电子在真空中被加速后,从金属板的小孔水平穿出,接着射入水平放置的两平行金属板间.已知两板的长度L=6.0cm,相距d=2cm,板间电压U=200V.求:(1)电子进入平行金属板间时的速度;
(2)电子射出平行金属板时竖直方向偏移的距离y;
(3)电子射出平行金属板时偏转的角度Φ.
分析 (1)由动能定理可以求出电子进入水平金属板时的速度.
(2)电子在水平板间做类平抛运动,应用类平抛运动规律可以求出竖直方向的偏移量.
(3)由类平抛运动规律可以求出速度偏角.
解答 解:(1)电子在加速电场中加速,由动能定理得:eU0=$\frac{1}{2}$mv02-0,
解得:v0=$\sqrt{\frac{2e{U}_{0}}{m}}$=$\sqrt{\frac{2×1.6×1{0}^{-19}×2500}{9.1×1{0}^{-31}}}$≈2.96×107m/s;
(2)电子在偏转电场中做类平抛运动,
在水平方向:L=v0t,
在竖直方向:y=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{eU}{md}$t2,
解得:y=$\frac{U{L}^{2}}{4d{U}_{0}}$=$\frac{200×(0.06)^{2}}{4×0.02×2500}$=0.0036m=0.36cm;
(3)速度偏角的正切值:tanΦ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\frac{eU}{md}×\frac{L}{{v}_{0}}}{{v}_{0}}$=$\frac{UL}{2d{U}_{0}}$=$\frac{200×0.06}{2×0.02×2500}$=0.12,则:Φarctan0.12;
答:(1)电子进入平行金属板间时的速度为2.96×107m/s;
(2)电子射出平行金属板时竖直方向偏移的距离y为0.36cm;
(3)电子射出平行金属板时偏转的角度Φ为arctan0.12.
点评 本题考查了电子在电场中的加速与偏转问题,分析清楚电子运动过程是正确解题的前提,应用动能定理、运动的合成与分解、牛顿第二定律与运动学公式可以解题.

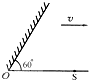 如图所示,一个点光源S通过平面镜成像.设光源不动,平面镜以速率v沿OS方向向光源移动,镜面与OS之间夹角恒为60°,则光源S的像S′(图中未画出)( )
如图所示,一个点光源S通过平面镜成像.设光源不动,平面镜以速率v沿OS方向向光源移动,镜面与OS之间夹角恒为60°,则光源S的像S′(图中未画出)( )| A. | 以速率v平行于OS向右运动 | B. | 以速率v垂直于OS向下运动 | ||
| C. | 以速率v沿SS′连线向S运动 | D. | 以速率$\sqrt{3}$v沿SS′连线向S运动 |
| A. | 1.6×1019 | B. | 6.25×1019 | C. | 1.60×1018 | D. | 6.25×1018 |
| A. | 同一直线上的两个匀变速直线运动的合运动一定是匀变速运动 | |
| B. | 不在同一直线的两个匀速直线运动的合运动可能是曲线运动 | |
| C. | 不在同一直线的两个匀变速直线运动的合运动一定是匀变速运动 | |
| D. | 水平方向匀速运动、竖直方向匀加速运动的合运动一定是平抛运动 |
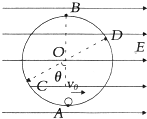 如图所示,在竖直平面内固定的圆形绝缘轨道的圆心在O点、半径为r,内壁光滑,A、B两点分别是圆弧的最低点和最高点.该区间存在方向水平向右的匀强电场,一质量为m、带负电的小球静止在C点,O、C连线与竖直方向的夹角θ=60°,重力加速度为g.
如图所示,在竖直平面内固定的圆形绝缘轨道的圆心在O点、半径为r,内壁光滑,A、B两点分别是圆弧的最低点和最高点.该区间存在方向水平向右的匀强电场,一质量为m、带负电的小球静止在C点,O、C连线与竖直方向的夹角θ=60°,重力加速度为g.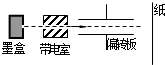 打印机是办公的常用工具,喷墨打印机是其中的一种.图是喷墨打印机的工作原理简化图.其中墨盒可以喷出半径约为10-5m的墨汁微滴,大量的墨汁微滴经过带电室时被带上负电荷,成为带电微粒.墨汁微滴所带电荷量的多少由计算机的输入信号按照文字的排列规律进行控制.带电后的微滴以一定的初速度进入由两块平行带电金属板形成的偏转电场中,微滴经过电场的作用发生偏转后打在纸面上,显示出字体.若某种喷墨打印机的偏转电场极板长度为l,两板间的距离为d,偏转电场极板的右端距纸面的距离为b,某个带电微滴的质量为m,沿两板间的中心线以初速度v0进入偏转电场.偏转电场两极板间电压为U.该微滴离开电场时的速度大小为v,不计微滴受到的重力和空气阻力影响,忽略电场边沿处场强的不均匀性.
打印机是办公的常用工具,喷墨打印机是其中的一种.图是喷墨打印机的工作原理简化图.其中墨盒可以喷出半径约为10-5m的墨汁微滴,大量的墨汁微滴经过带电室时被带上负电荷,成为带电微粒.墨汁微滴所带电荷量的多少由计算机的输入信号按照文字的排列规律进行控制.带电后的微滴以一定的初速度进入由两块平行带电金属板形成的偏转电场中,微滴经过电场的作用发生偏转后打在纸面上,显示出字体.若某种喷墨打印机的偏转电场极板长度为l,两板间的距离为d,偏转电场极板的右端距纸面的距离为b,某个带电微滴的质量为m,沿两板间的中心线以初速度v0进入偏转电场.偏转电场两极板间电压为U.该微滴离开电场时的速度大小为v,不计微滴受到的重力和空气阻力影响,忽略电场边沿处场强的不均匀性. A、B是水平放置的平行板电容器,当A、B两板直接接到电源两极时,一电子从A板由静止飞到B板时的速度为v0.电源内阻r=1Ω,R1=4Ω,现若按图示连接,当开关S闭合时,电子从A板由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{1}{2}$v0,当开关S断开时,电子从A板由静止飞向B板经C点时的速度为$\frac{\sqrt{3}}{3}$v0,求R2和R3的阻值.
A、B是水平放置的平行板电容器,当A、B两板直接接到电源两极时,一电子从A板由静止飞到B板时的速度为v0.电源内阻r=1Ω,R1=4Ω,现若按图示连接,当开关S闭合时,电子从A板由静止飞到B板的过程中,通过两板的中点C的速度为$\frac{1}{2}$v0,当开关S断开时,电子从A板由静止飞向B板经C点时的速度为$\frac{\sqrt{3}}{3}$v0,求R2和R3的阻值.