题目内容
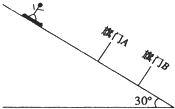 滑降赛是冬季奥运会高山滑雪项目中的一个小项.如图是简化后滑降赛的雪道示意图,一运动员脚踏长L=1.6m的雪板从倾角为30°的雪道上由静止开始匀加速下滑,滑雪板先后穿过用旗杆插成的两个旗门A,B,所用时间分别为t1=0.4s和t2=0.1s已知滑雪板与雪道之间的动摩擦因数μ=
滑降赛是冬季奥运会高山滑雪项目中的一个小项.如图是简化后滑降赛的雪道示意图,一运动员脚踏长L=1.6m的雪板从倾角为30°的雪道上由静止开始匀加速下滑,滑雪板先后穿过用旗杆插成的两个旗门A,B,所用时间分别为t1=0.4s和t2=0.1s已知滑雪板与雪道之间的动摩擦因数μ=
| ||
| 15 |
分析:由牛顿第二定律可得人的加速度,由滑雪板通过旗门的时间可得滑雪板接触旗门时的速度,进而由运动学可解旗门AB距离.
解答:解:滑雪板从雪道上滑下,由牛顿第二定律:
mgsinθ-μmgcosθ=ma
解得:a=gsinθ-μgcosθ=10×
-
×10×
=4m/s2
滑雪板前端到达旗门A时的速度为v1,由运动学:
L=v1t1+
a t12
解得:v1=
-
at1=
-
×4×0.4=3.2m/s
滑雪板前端到达旗门B时的速度为v2,由运动学:
L=v2t2+
a t22
解得:v2=
-
at2=
-
×4×0.1=15.8m/s
滑雪板由A门到B门,由运动学可得:
v22-v12=2as
联立解得:s=
m=30m
答:两个旗门AB之间的距离为30m.
mgsinθ-μmgcosθ=ma
解得:a=gsinθ-μgcosθ=10×
| 1 |
| 2 |
| ||
| 15 |
| ||
| 2 |
滑雪板前端到达旗门A时的速度为v1,由运动学:
L=v1t1+
| 1 |
| 2 |
解得:v1=
| L |
| t1 |
| 1 |
| 2 |
| 1.6 |
| 0.4 |
| 1 |
| 2 |
滑雪板前端到达旗门B时的速度为v2,由运动学:
L=v2t2+
| 1 |
| 2 |
解得:v2=
| L |
| t2 |
| 1 |
| 2 |
| 1.6 |
| 0.1 |
| 1 |
| 2 |
滑雪板由A门到B门,由运动学可得:
v22-v12=2as
联立解得:s=
| 15.82-3.22 |
| 2×4 |
答:两个旗门AB之间的距离为30m.
点评:这是运动学公式的反复应用,很多题目都是这样,依据给定的过程,仔细分析,基本就是颠来倒去的应用那几个基本公式就可以解题,关键是做好运动分析.

练习册系列答案
相关题目
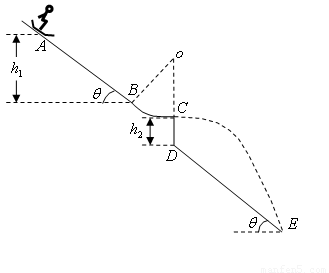
 、跳台、着陆坡、终止区组成。运动员脚着专用滑雪板,从起滑台起滑,在助滑道下滑加速后起跳,于台端飞出,沿抛物线在空中飞行一段时间后,落在着陆坡上继续滑行,最后停止在终止区。如图为一跳台滑雪场地,助滑坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=10m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差h1=35m,竖直跳台CD高度差为h2=5m,跳台底端与倾角为37°斜坡DE相连。运动员连同滑雪装备总质量为80kg,从A点由静止滑下,通过C点直接飞到空中,飞行一段时间落到着陆坡上,测得着陆坡上落点E到D点距离为125m(小计空气阻力,g取10m/s2。,sin37°=0.6,cos37°=0.8)。求:
、跳台、着陆坡、终止区组成。运动员脚着专用滑雪板,从起滑台起滑,在助滑道下滑加速后起跳,于台端飞出,沿抛物线在空中飞行一段时间后,落在着陆坡上继续滑行,最后停止在终止区。如图为一跳台滑雪场地,助滑坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=10m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差h1=35m,竖直跳台CD高度差为h2=5m,跳台底端与倾角为37°斜坡DE相连。运动员连同滑雪装备总质量为80kg,从A点由静止滑下,通过C点直接飞到空中,飞行一段时间落到着陆坡上,测得着陆坡上落点E到D点距离为125m(小计空气阻力,g取10m/s2。,sin37°=0.6,cos37°=0.8)。求: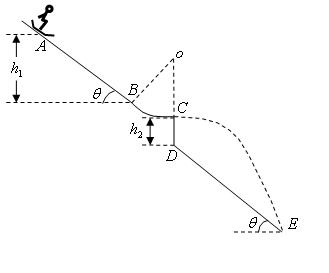
 的速度大小
的速度大小