Question

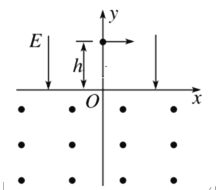
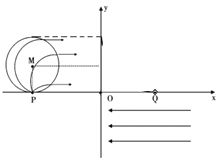
【题目】如图所示，在第二象限内存在一个半径为a的圆形有界匀强磁场，磁场圆心坐标。在位置坐标为的P点存在一个粒子发射源，能在纸面内的第二象限向各个方向发射质量为m、带电量的粒子，其速度大小均为v。这些粒子经过圆形磁场后都可以垂直y轴进入第一象限，并经过第一象限内一个垂直xOy平面向外的有界匀强磁场区域，该区域磁场的磁感应强度大小为第二象限圆形磁场区域内磁感应强度大小的二分之一，粒子经过该磁场后，全部汇聚到位置坐标为的Q点，再从Q点进入第四象限，第四象限内有大小为、方向水平向左的匀强电场。不计粒子重力，求：

（1）第二象限圆形有界匀强磁场的磁感应强度；

（2）第一象限有界磁场的最小面积；

（3）这些粒子经过匀强电场后再次经过y轴时速度的大小以及粒子所能达到的最远位置坐标。

Answer 1

【答案】（1） （2） （3）3v；（0，）

【解析】

（1）要想使这些粒子经过圆形磁场后都可以垂直y轴进入第一象限，则粒子在圆形磁场中做匀速圆周运动的半径必须和圆形磁场的半径相同，即：

R=a

在磁场中，由洛仑兹力提供向心力：

联立可得：

由左手定则知：磁感应强度B的方向垂直xOy平面向外
（2）第一象限区域磁场的磁感应强度大小为第二象限圆形磁场区域内磁感应强度大小的二分之一，则根据

此时粒子在磁场中做圆周运动的半径为

R′=2a

则最小磁场的直径为

最小面积为

（3）粒子在从P到Q运动的过程中，所经历的磁场区域均不可以改变其速度的大小，所有粒子在到达Q点的速度仍是v。虽然不同粒子在Q点的速度方向不同，从Q到y轴负方向，
由动能定理可得：

解得：

由第一象限内的磁场分布可以知道，所有从Q点射出的粒子，其速度大小均为v，方向颁布在沿x轴正向与y轴负向之间的90°范围之内。
现研究从Q点射出的，速度与y轴负向平角为θ的粒子。其轨迹应是类斜抛。则有

y=v cosθ×t

联立两式，消去θ可得：

从此式可以看出：
当时，

故第二次经过y轴最远位置坐标为：（0，）