题目内容
19.如图甲所示,以小车为研究对象,探究拉力做功与动能变化的关系实验中: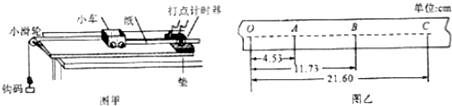
(1)下列说法正确的是BCD.
A、平衡摩擦力时必须将钩码通过细线挂在小车上
B、为减小系统误差,应使钩码质量远小于小车质量
C、实验时,应使小车靠近打点计时器由静止释放
D、调整滑轮高度,使细线与木块平行
(2)图乙是实验中获得的一条纸带的一部分,选取O、A、B、C计数点,已知打点计时器使用的交流电频率为50Hz,则打B点时小车的瞬时速度大小为0.854m/s(保留三位有效数字)
(3)在满足(1)条件下,若钩码质量为m,小车质量为M,A、B两点间距为x,速度分别为vA和vB,则探究结果的表达式为mgx=$\frac{1}{2}$MvB2-$\frac{1}{2}$MvA2.
分析 (1)平衡摩擦力是用重力的下滑分量来平衡小车受到的摩擦力,故不应该将钩码通过细线挂在小车上,为减小系统误差,应使钩码质量远小于小车质量,实验时,应使小车靠近打点计时器由静止释放;
(2)用平均速度等于中间时刻的瞬时速度的结论求解;
(3)细线的拉力近似等于沙和沙桶的总重力,需要验证的方程是细线对滑块做功与滑块动能的增加的关系,细线对滑块做功等于沙和沙桶重力势能的减小量,根据动能定理分析答题.
解答 解:(1)A、平衡摩擦力时要将纸带、打点计时器、小车等连接好,但不要通电和挂钩码,故A错误;
B、为减小系统误差,应使钩码质量远小于小车质量,使系统的加速度较小,避免钩码失重的影响,故B正确;
C、实验时,应使小车靠近打点计时器由静止释放,故C正确;
D、为了使绳子的拉力充当小车运动的合力,应使滑轮高度使细绳与长木板表面平行,故D正确.
故选:BCD;
(2)B为AC时间段的中间时刻,根据匀变速运动规律得,平均速度等于中间时刻的瞬时速度,故:vB=$\frac{{x}_{AC}}{2T}=\frac{0.216-0.0453}{0.2}=0.854m/s$
(3)由动能定理得:mgx=$\frac{1}{2}$MvB2-$\frac{1}{2}$MvA2,则探究结果的表达式为mgx=$\frac{1}{2}$MvB2-$\frac{1}{2}$MvA2.
故答案为:(1)BCD;(2)0.854;(3)mgx=$\frac{1}{2}$MvB2-$\frac{1}{2}$MvA2
点评 “探究恒力做功与动能改变的关系”与“探究加速度与力、质量的关系”有很多类似之处,在平时学习中要善于总结、比较,提高对实验的理解能力.

练习册系列答案
相关题目
10.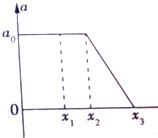 放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
 放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )
放在水平面上的物体,在力F作用下开始运动,以物体静止时的位置为坐标原点,力F的方向为正方向建立x轴,物体的加速度随位移的变化图象如图所示.下列说法中错误的是( )| A. | 0~x2过程中物体做匀加速直线运动,x2~x3过程中物体做匀减速运动 | |
| B. | 位移为x1时,物体的速度大小为$\sqrt{2{a}_{0}{x}_{1}}$ | |
| C. | 位移为x2时,物体的速度达到最大 | |
| D. | 物体的最大速度为$\sqrt{{a}_{0}({x}_{2+}{x}_{3})}$ |
7.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,速度减小为原来的$\frac{1}{2}$,则变轨前、后卫星的( )
| A. | 轨道半径之比为1:4 | B. | 向心力之比为4:1 | ||
| C. | 周期之比为1:8 | D. | 变轨道后的机械能减少 |
14.已知月球绕地球公转的周期为T,地球半径为R,地球表面的重力加速度为g,则月球绕地球公转的线速度大小为( )
| A. | $\root{3}{\frac{2πg{R}^{2}}{T}}$ | B. | $\root{3}{\frac{πg{R}^{2}}{2T}}$ | C. | 2$\root{3}{\frac{πg{R}^{2}}{T}}$ | D. | $\frac{1}{2}$$\root{3}{\frac{πg{R}^{2}}{T}}$ |
4.已知质量分别均匀的球壳对其内部物体的引力为零.科学家设想在赤道正上方高d处和正下方深为d处各修建一环形轨道,轨道面与赤道面共面.现有A、B两物体分别在上述两轨道中做匀速圆周运动,若地球半径为R,轨道对它们均无作用力,则两物体运动的向心加速度大小、线速度大小、角速度、周期之比为( )
| A. | $\frac{{a}_{A}}{{a}_{B}}$=($\frac{R-d}{R+d}$)2 | B. | $\frac{{v}_{A}}{{v}_{B}}$=$\sqrt{\frac{R-d}{R+d}}$ | ||
| C. | $\frac{{ω}_{A}}{{ω}_{B}}$=$\sqrt{\frac{(R-d)^{3}}{(R+d)^{3}}}$ | D. | $\frac{{T}_{A}}{{T}_{B}}$=$\sqrt{\frac{(R+d)^{3}}{{R}^{3}}}$ |
11. 在绝缘水平桌面上放置如图所示的电路,abdc为一质量为m形状为长方体的金属导体电阻,电阻阻值为R,长度ab=x、宽度ac=L、厚度为d,电源电动势为E、内阻为r,空间内存在竖直向下、磁感强度为B的匀强磁场,接通电源后电阻不滑动,(已知此电阻单位体积内有n个载流子,每个载流子的电荷量为e),以下分析错误的是( )
在绝缘水平桌面上放置如图所示的电路,abdc为一质量为m形状为长方体的金属导体电阻,电阻阻值为R,长度ab=x、宽度ac=L、厚度为d,电源电动势为E、内阻为r,空间内存在竖直向下、磁感强度为B的匀强磁场,接通电源后电阻不滑动,(已知此电阻单位体积内有n个载流子,每个载流子的电荷量为e),以下分析错误的是( )
 在绝缘水平桌面上放置如图所示的电路,abdc为一质量为m形状为长方体的金属导体电阻,电阻阻值为R,长度ab=x、宽度ac=L、厚度为d,电源电动势为E、内阻为r,空间内存在竖直向下、磁感强度为B的匀强磁场,接通电源后电阻不滑动,(已知此电阻单位体积内有n个载流子,每个载流子的电荷量为e),以下分析错误的是( )
在绝缘水平桌面上放置如图所示的电路,abdc为一质量为m形状为长方体的金属导体电阻,电阻阻值为R,长度ab=x、宽度ac=L、厚度为d,电源电动势为E、内阻为r,空间内存在竖直向下、磁感强度为B的匀强磁场,接通电源后电阻不滑动,(已知此电阻单位体积内有n个载流子,每个载流子的电荷量为e),以下分析错误的是( )| A. | 电阻内电流大小I=$\frac{E}{R+r}$ | |
| B. | 电阻上a点和c点间电势差为Uac=-$\frac{EB}{n(R+r)de}$ | |
| C. | 水平桌面和电阻间的动摩擦因数应大于$\frac{BEx}{mg(R+r)}$ | |
| D. | 金属导体电阻中的正电荷向右移动,电子向左移动 |
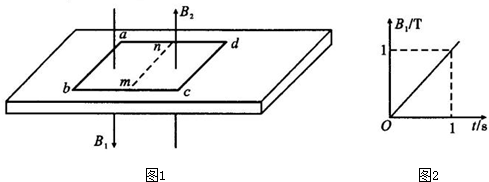
8.将一质量为M=2kg的绝缘长木板固定在水平面上,一正方形导线框abcd放在绝缘长木板上,正方形导线框的质量为m=1kg,边长L=1m,电阻R=0.1Ω,以过bc边的中垂线mn为边界,如图1所示,由t=0时刻开始在mn左侧的线框区域内加一竖直向下的磁场,其磁感应强度随时间的变化规律如图2所示,在mn右侧的线框区域内加一竖直向上、磁感应强度为B2=0.5T的匀强磁场,线框abcd的四边为磁场的边界.若导线框与长板间的最大静摩擦力等于滑动摩擦力,它们之间的动摩擦因数μ=0.3,g=10m/s2,则下列说法正确的是( )

| A. | 导线框中的感应电动势为0.5V | |
| B. | 在t=1s时,导线框所受的安培力大小为1N,方向水平向左 | |
| C. | 导线框中产生俯视逆时针方向的感应电流 | |
| D. | 在0-1s内,导线框一直静止在绝缘长板上 |
9.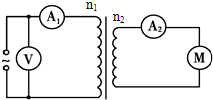 如图所示,一理想变压器原副线圈匝数分别为n1=1000匝.n2=200匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V).副线圈中接一电动机,电阻为11Ω,电流表A2示数为1A,电表对电路的影响忽略不计.下列说法正确的是( )
如图所示,一理想变压器原副线圈匝数分别为n1=1000匝.n2=200匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V).副线圈中接一电动机,电阻为11Ω,电流表A2示数为1A,电表对电路的影响忽略不计.下列说法正确的是( )
 如图所示,一理想变压器原副线圈匝数分别为n1=1000匝.n2=200匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V).副线圈中接一电动机,电阻为11Ω,电流表A2示数为1A,电表对电路的影响忽略不计.下列说法正确的是( )
如图所示,一理想变压器原副线圈匝数分别为n1=1000匝.n2=200匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V).副线圈中接一电动机,电阻为11Ω,电流表A2示数为1A,电表对电路的影响忽略不计.下列说法正确的是( )| A. | 此交流电的频率为100 Hz | B. | 电流表A1示数为5 A | ||
| C. | 电压表示数为220$\sqrt{2}$V | D. | 此电动机输出功率为33 W |