题目内容
【题目】如图所示，真空中有以O′为圆心、r为半径的圆柱形匀强磁场区域，圆的最下端与x轴相切于坐标原点O，圆的右端与平行于y轴的虚线MN相切，磁感应强度为B，方向垂直纸面向外，在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场。现从坐标原点O向纸面内不同方向发射速率相同的质子，质子在磁场中做匀速圆周运动的半径也为r，已知质子的电荷量为e，质量为m，不计质子的重力、质子对电磁场的影响及质子间的相互作用力。求：
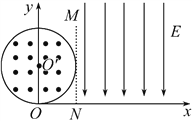
（1）质子进入磁场时的速度大小；
（2）画出沿y轴正方向射入磁场的质子到达x轴的运动轨迹；
（3）沿y轴正方向射入磁场的质子到达x轴所需的时间和到达 x轴的位置坐标。
【答案】（1）v=
（2）
（3）t= 
+
；（Br
【解析】(1)由洛伦兹力公式和牛顿第二定律得：Bev= m
解得：v=
（2）沿y轴正方向射入磁场的质子到达x轴的运动轨迹如图所示；
（3）质子沿y轴正方向射入磁场，则以N为圆心转过1/4 圆弧后从A点垂直电场方向进入电场，质子在磁场中有：T=
质子在磁场中的运动时间tB 
=
进入电场后质子做类平抛运动，y方向上的位移 y=r=
atE2
X方向上的位移 x=vtE
由牛顿第二定律得 Ee=ma
解得：tE=
x=Br
则粒子到达x轴所需的时间t=tB+tE = 
+
粒子到达x轴的坐标为（Br
【题目】某同学采用图甲的实验电路测绘小灯泡的伏安特性曲线的记录数据如下表：
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
U/V | 0 | 0.80 | 1.50 | 1.80 | 2.20 | 2.60 | 3.00 |
I/A | 0 | 0.080 | 0.150 | 0.170 | 0.190 | 0.200 | 0.205 |
（1）请按图甲所给的电路，在中间的实物图中将电压表接入电路_____（用实线表示导线）。
（2）图甲中滑动变阻器采用了______接法，闭合开关S之前，滑动变阻器的滑片P应处在最_____端；当滑片从最左端向右滑动时，可让A、B间的电压从__________开始逐渐___________。
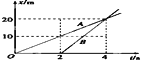
（3）请在右边的坐标纸上描点，并描绘出小灯泡的伏安特性曲线______。
（4）根据画出的曲线可以看出小灯泡的电阻随所加电压的增大而_______，发生这种变化的原因是
__________________________________________________________。
（5）对图甲所示的测量电路，以下分析正确的是（_______）
A.此接法中电流表的内阻越小，测量越精确
B.此接法中电压表的内阻越大，测量越精确
C.此接法中由于电流表的分压作用，使电压表的读数大于灯泡两端真实电压，RL的测量值大于真实值
D.此接法中由于电压表的分流作用，使电流表的读数大于通过灯泡的真实电流，RL的测量值小于真实值
