题目内容
【题目】如图,与水平面夹角θ=37°的斜面和半径R=0.4m的光滑圆轨道相切于B点,且固定于竖直平面内。滑块从斜面上的A点由静止释放,经B点后沿圆轨道运动,通过最高点C时轨道对滑块的弹力为零。已知滑块与斜面间动摩擦因数μ=0.25。(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
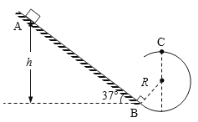
(1)滑块在B点的速度大小vB
(2)A、B两点间的高度差h
【答案】(1)4.3m/s(2)1.4m
【解析】
对滑块在C点应用牛顿第二定律求出滑块在C点的速度大小,对滑块从B到C应用机械能守恒即可求得在B处的速度;对滑块从A到B应用动能定理即可求出A、B两点间的高度差;
解:(1)通过最高点C时轨道对滑块的弹力为零
对滑块在C点应用牛顿第二定律可得:![]()
所以![]()
滑块在光滑圆轨道上运动,机械能守恒,故有:
![]()
所以,![]()
(2) 滑块从A到B只有重力、摩擦力做功,故由动能定理可得:![]()
所以![]()

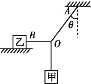
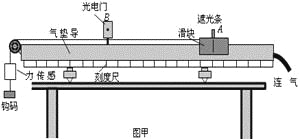
【题目】如图甲所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,滑块上固定一遮光条,滑块用细线绕过气垫导轨左端的定滑轮与力传感器相连,力传感器可直接测出绳中拉力,传感器下方悬挂钩码,每次滑块都从A处由静止释放。气垫导轨摩擦阻力很小可忽略不计,由于遮光条的宽度很小,可认为遮光条通过光电门时速度不变。
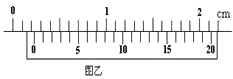
(1)该同学用游标卡尺测量遮光条的宽度d,如图乙所示,则d= mm.
(2)实验时,该同学用游标卡尺测量遮光条的宽度d,将滑块从A位置由静止释放,测量遮光条到光电门的距离L,若要得到滑块的加速度,还需由数字计时器读出遮光条通过光电门B的 ;
(3)下列不必要的一项实验要求是( )。
A.应使滑块质量远大于钩码和力传感器的总质量 |
B.应使A位置与光电门间的距离适当大些 |
C.应将气垫导轨调节水平 |
D.应使细线与气垫导轨平行 |
(4)改变钩码质量,测出对应的力传感器的示数F,已知滑块总质量为M,用(2)问中已测物理量和已给物理量写出M和F间的关系表达式F= 。