题目内容
13.宇航员站在一个星球表面的某高处,以水平初速度抛出一个小球.经过时间t,小球落到星球表面,测得抛出点与落地点的距离为L,与地面的夹角为θ,已知该星球的半径为R,万有引力常数为G,若发射一颗在该星球表面附近绕该星球做匀速圆周运动的卫星,求这颗卫星的速度.分析 根据几何关系求出平抛运动下落的高度,根据竖直方向做自由落体运动求出重力加速度大小,根据万有引力等于重力提供向心力求出这颗卫星的速度.
解答 解:根据几何关系可得:$\sqrt{{x}^{2}+{h}^{2}}=L$,$tanθ=\frac{h}{x}$,
解得:h=$Ltanθ\sqrt{\frac{1}{tanθ+1}}$
物体做平抛运动时,h=$\frac{1}{2}g{t}^{2}$,
解得:g=$\frac{2Ltanθ\sqrt{\frac{1}{tanθ+1}}}{{t}^{2}}$
在地球表面万有引力等于重力,根据重力提供向心力,则有
m$\frac{{v}^{2}}{R}=mg$
解得:v=$\sqrt{\frac{2RLtanθ\sqrt{\frac{1}{tanθ+1}}}{{t}^{2}}}$
答:这颗卫星的速度为$\sqrt{\frac{2RLtanθ\sqrt{\frac{1}{tanθ+1}}}{{t}^{2}}}$.
点评 解决本题的关键掌握万有引力等于重力、万有引力提供向心力这两个重要理论,并能灵活运用,并能结合几何求解,难度适中.

练习册系列答案
相关题目
18.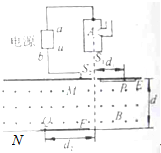 如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子气体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电中性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经A与E两极板间电压为u的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿着垂直磁场方向进入磁感应强度大小为B方向垂直纸面向外的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当电源两极性不同时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F水平底片上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm,不计空气阻力、带电粒子所受重力以及带电粒子之间的相互作用可忽略不计.下列说法中正确的是( )
如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子气体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电中性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经A与E两极板间电压为u的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿着垂直磁场方向进入磁感应强度大小为B方向垂直纸面向外的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当电源两极性不同时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F水平底片上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm,不计空气阻力、带电粒子所受重力以及带电粒子之间的相互作用可忽略不计.下列说法中正确的是( )
 如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子气体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电中性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经A与E两极板间电压为u的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿着垂直磁场方向进入磁感应强度大小为B方向垂直纸面向外的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当电源两极性不同时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F水平底片上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm,不计空气阻力、带电粒子所受重力以及带电粒子之间的相互作用可忽略不计.下列说法中正确的是( )
如图所示装置可用来分析气体原子的组成.首先使待研究气体进入电离室A,在此气体被电离成等离子气体(待研究气体的等离子体由含有一价正离子和电荷量为e的电子组成,整体显电中性).这些等离子体(统称“带电粒子”)从电离室下端狭缝S1飘出(忽略飘出的速度),经A与E两极板间电压为u的加速电场后(忽略这些带电粒子被加速的时间),从狭缝S2沿着垂直磁场方向进入磁感应强度大小为B方向垂直纸面向外的有界匀强磁场,在磁场的上、下边界处分别装有水平底片E和F.当电源两极性不同时,发现从电离室狭缝S1飘出的带电粒子分别打在E和F水平底片上的P、Q点.已知狭缝S2与水平底片E上P点之间的距离d1=2.0cm,到水平底片F上Q点的水平距离d2=6.4cm,磁场区域宽度d=30cm,不计空气阻力、带电粒子所受重力以及带电粒子之间的相互作用可忽略不计.下列说法中正确的是( )| A. | 当电源上极板a为负极时,负离子打在P点 | |
| B. | 打在P点离子质量为m1=$\frac{{d}_{1}^{2}{B}^{2}e}{2u}$ | |
| C. | 打在Q点离子在磁场中运动时间比打在P点离子在磁场中运动时间短 | |
| D. | 打在Q点离子质量一定比打在P点离子质量大 |
5. 如图所示,一个矩形金属线框abcd与条形磁铁的中轴线OO′在同一平面 内.下列能产生感应电流的操作是( )
如图所示,一个矩形金属线框abcd与条形磁铁的中轴线OO′在同一平面 内.下列能产生感应电流的操作是( )
 如图所示,一个矩形金属线框abcd与条形磁铁的中轴线OO′在同一平面 内.下列能产生感应电流的操作是( )
如图所示,一个矩形金属线框abcd与条形磁铁的中轴线OO′在同一平面 内.下列能产生感应电流的操作是( )| A. | 使线框以OO′为轴转动 | B. | 使线框以ab边为轴转动 | ||
| C. | 使线框以bc边为轴转动 | D. | 使线框向右加速平移 |
2.下列各种运动中,机械能守恒的是( )
| A. | 跳伞运动员在空中匀速下降时 | |
| B. | 用绳拉着一个物体匀速上升时 | |
| C. | 一物体以某初速度沿光滑曲面下滑时 | |
| D. | 物体在空中以0.9g的加速度匀加速下落时 |
3. 如图,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做竖直面内的圆周运动,若小球通过轨道最低点a处的速度为va=4m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则通过最低点和最高点时,细杆对小球作用力的情况是( )
如图,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做竖直面内的圆周运动,若小球通过轨道最低点a处的速度为va=4m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则通过最低点和最高点时,细杆对小球作用力的情况是( )
 如图,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做竖直面内的圆周运动,若小球通过轨道最低点a处的速度为va=4m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则通过最低点和最高点时,细杆对小球作用力的情况是( )
如图,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做竖直面内的圆周运动,若小球通过轨道最低点a处的速度为va=4m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则通过最低点和最高点时,细杆对小球作用力的情况是( )| A. | a处方向竖直向下,大小为126N | B. | a处方向竖直向上,大小为126N | ||
| C. | b处方向竖直向下,大小为6N | D. | b处方向竖直向上,大小为6N |
 五个直径均为d=5cm的圆环连接在一起,用细绳悬于o点,枪管水平时枪口中心与第五个环心在同一水面上,如图,它们相距100m,且连线与球面垂直.现烧断细线,经过0.1s后开枪射出子弹,若子弹恰好穿过第2个环的环心,求子弹离开枪口的速度.
五个直径均为d=5cm的圆环连接在一起,用细绳悬于o点,枪管水平时枪口中心与第五个环心在同一水面上,如图,它们相距100m,且连线与球面垂直.现烧断细线,经过0.1s后开枪射出子弹,若子弹恰好穿过第2个环的环心,求子弹离开枪口的速度. 如图所示,在第Ⅲ象限存在着沿y轴正方向的匀强电场,在第Ⅰ、Ⅳ象限存在着半径为a的圆形磁场区域,磁场方向垂直纸面向里,该区域的一条直径与x轴共线,一带正电的粒子初速度为v0,质量为m,电荷量为q,从A点(-l,-$\frac{\sqrt{3}}{6}l$)垂直于电场线方向进入匀强电场,结果从坐标原点O进入圆形磁场区域,已知圆形磁场区域的磁感应强度为$\frac{2\sqrt{3}m{v}_{0}}{3aq}$,并且粒子第一次到达磁场区域的边界时恰因某种原因被反向弹回(能量孙素忽略不计),最终粒子第二次到达磁场的边界时从磁场中穿出,粒子重力不计,求:
如图所示,在第Ⅲ象限存在着沿y轴正方向的匀强电场,在第Ⅰ、Ⅳ象限存在着半径为a的圆形磁场区域,磁场方向垂直纸面向里,该区域的一条直径与x轴共线,一带正电的粒子初速度为v0,质量为m,电荷量为q,从A点(-l,-$\frac{\sqrt{3}}{6}l$)垂直于电场线方向进入匀强电场,结果从坐标原点O进入圆形磁场区域,已知圆形磁场区域的磁感应强度为$\frac{2\sqrt{3}m{v}_{0}}{3aq}$,并且粒子第一次到达磁场区域的边界时恰因某种原因被反向弹回(能量孙素忽略不计),最终粒子第二次到达磁场的边界时从磁场中穿出,粒子重力不计,求: