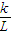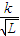题目内容
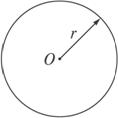
一圆柱形飞船的横截面半径为r，使这飞船绕中心轴O自转，从而给飞船内的物体提供了“人工重力”．若飞船绕中心轴O自转的角速度为ω，那么“人工重力”中的“重力加速度g”的值与离开转轴O的距离L的关系是（其中k为比例系数）（ ）
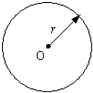
A．g=k
| B．g=kL | C．g=
| D．g=
|
圆环匀速转动后，宇航员是靠环对他的支持力提供向心力的，这时宇航员会压紧环，相当于宇航员受到的等效重力方向是背离中心轴O，等效重力的大小等于环对人的支持力（在里面看，人是“静止”的，所以“重力”大小等于支持力）．
即 G效=F支=F向=m
等效重力 G效=mg
所以等效的重力加速度是 g=ω2r=ω2L
因为圆环的半径是确定的，所以 g=kL，故ACD错误，B正确．
故选B．
即 G效=F支=F向=m
| v2 |
| r |
所以等效的重力加速度是 g=ω2r=ω2L
因为圆环的半径是确定的，所以 g=kL，故ACD错误，B正确．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
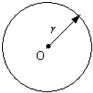一圆柱形飞船的横截面半径为r，使这飞船绕中心轴O自转，从而给飞船内的物体提供了“人工重力”．若飞船绕中心轴O自转的角速度为ω，那么“人工重力”中的“重力加速度g”的值与离开转轴O的距离L的关系是（其中k为比例系数）（ ）
B.g=kL C.
D.
