题目内容
 (2011?天津)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求:
(2011?天津)如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求:(1)粘合后的两球从飞出轨道到落地的时间t;
(2)小球A冲进轨道时速度v的大小.
分析:(1)求平抛运动的时间,当然是从竖直方向的自由落体运动中求得.
(2)小球A以某一初速度冲进轨道,到达半圆轨道最高点的过程机械能守恒、A与B碰撞过程动量守恒,而碰撞完成后的速度就是AB一起平抛的初速度.列出机械能守恒和动量守恒的方程组,问题可解.
(2)小球A以某一初速度冲进轨道,到达半圆轨道最高点的过程机械能守恒、A与B碰撞过程动量守恒,而碰撞完成后的速度就是AB一起平抛的初速度.列出机械能守恒和动量守恒的方程组,问题可解.
解答:解:(1)粘合后的两球飞出轨道后做平抛运动,竖直方向分运动为自由落体运动,
有2R=
gt2…①
解得t=2
…②
(2)设球A的质量为m,碰撞前速度大小为v1,把球A冲进轨道最低点时的重力势能定为0,由机械能守恒定律知
mv2=
m
+2mgR…③
设碰撞后粘合在一起的两球速度大小为v2,则v2=
=
由动量守恒定律知 mv1=2mv2…④
飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有 2R=v2t…⑤
综合②③④⑤式得v=2
答:(1)两球从飞出轨道到落地的时间t=2
(2)小球A冲进轨道时速度为2
.
有2R=
| 1 |
| 2 |
解得t=2
|
(2)设球A的质量为m,碰撞前速度大小为v1,把球A冲进轨道最低点时的重力势能定为0,由机械能守恒定律知
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
设碰撞后粘合在一起的两球速度大小为v2,则v2=
| 2R |
| t |
| gR |
由动量守恒定律知 mv1=2mv2…④
飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有 2R=v2t…⑤
综合②③④⑤式得v=2
| 2gR |
答:(1)两球从飞出轨道到落地的时间t=2
|
(2)小球A冲进轨道时速度为2
| 2gR |
点评:本题考查机械能守恒和动量守恒,分段列出相应的物理规律方程是解决问题的关键,

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
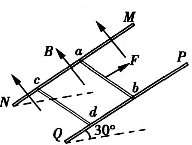 (2011?天津)如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问:
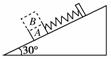
(2011?天津)如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问: (2011?天津)如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B受到的摩擦力( )
(2011?天津)如图所示,A、B两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B受到的摩擦力( ) (2011?天津模拟)如图所示,把长为L的导体棒置于竖直向下的匀强磁场中,磁场的磁感应强度为B,导体棒与磁场方向垂直,棒中通有电流I,则导体棒所受安培力的大小为
(2011?天津模拟)如图所示,把长为L的导体棒置于竖直向下的匀强磁场中,磁场的磁感应强度为B,导体棒与磁场方向垂直,棒中通有电流I,则导体棒所受安培力的大小为