题目内容
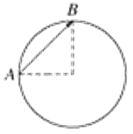
【题目】2018年6月14日,我国探月工程嫦娥四号“鹊桥”中继星进入地月拉格朗日L2点的Halo使命轨道,以解决月球背面的通讯问题。如图所示,地月拉格朗日L2点在地球与月球的连线上。若“鹊桥”中继星在地月拉格朗日L2点上,受地球、月球两大天体的引力作用,其绕地球运行的周期和月球绕地球运行的周期相同。已知地球质量、地月距离和月球的质量,分析月球受力时忽略“鹊桥”中继星对月球的作用力,则下列物理量可以求出的是( )

A.引力常量B.月球绕地球运行的周期
C.“鹊桥”中继星的质量D.地月拉格朗日L2点与地球间的距离
【答案】D
【解析】
设“鹊桥”中继星的质量为m,它绕地球做圆周运动的向心力由地球和月球的引力的合力提供,设它做圆周运动的周期和月球绕地球运行的周期为T,地月拉格朗日L2点与地球间的距离为r,由万有引力定律可得:
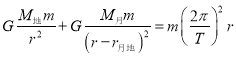 ,
,
对月球:
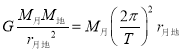 ,
,
联立解得:
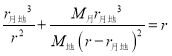
若已知地球质量、地月距离和月球的质量,则可求出地月拉格朗日L2点与地球间的距离。
A.引力常量.故A不符合题意.
B.月球绕地球运行的周期.故B不符合题意.
C.“鹊桥”中继星的质量.故C不符合题意.
D.地月拉格朗日L2点与地球间的距离.故D符合题意.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为![]() ,完成下面问题。
,完成下面问题。
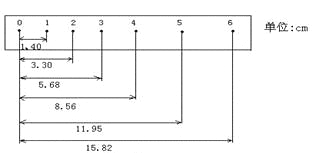
(1)根据打点计时器打出的纸带,我们可以直接得到的物理量是
A.时间间隔 | B.加速度 |
C.瞬时速度 | D.平均速度 |
(2)根据纸带上各个测量点间的距离,某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算
并填入表中,请你将4点对应的时刻的瞬时速度填入表中;(要求保留3位有效数字)
瞬时速度 | v1 | v2 | v3 | v4 | v5 |
数值(m/s) | 0.165 | 0.214 | 0.263 | 0.363 |
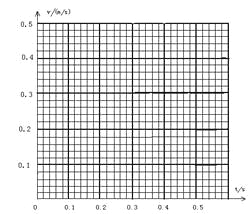
(3)在图所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线。
(4)由图像求出小车的加速度![]()