题目内容
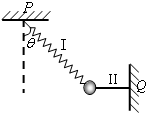 如图所示,质量m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小T1,Ⅱ中拉力大小T2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )
如图所示,质量m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小T1,Ⅱ中拉力大小T2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )分析:先研究原来静止的状态,由平衡条件求出弹簧和细线的拉力.刚剪短细绳时,弹簧来不及形变,故弹簧弹力不能突变;细绳的形变是微小形变,在刚剪短弹簧的瞬间,细绳弹力可突变!根据牛顿第二定律求解瞬间的加速度.
解答:解:A、C、绳子未断时,受力如图,由共点力平衡条件得,T2=mgtanθ,T1=
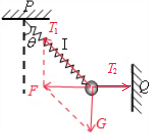
刚剪断弹簧Ⅰ瞬间,细绳弹力突变为0,故小球只受重力,加速度为g,竖直向下,故A错误,C错误;
B、D刚剪短细线瞬间,弹簧弹力和重力不变,受力如图
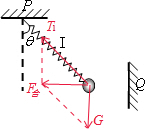
由几何关系,F合=T1sinθ=T2=ma,因而a=
=
,方向水平向左,故B正确,D错误.
故选B.
| mg |
| sinθ |

刚剪断弹簧Ⅰ瞬间,细绳弹力突变为0,故小球只受重力,加速度为g,竖直向下,故A错误,C错误;
B、D刚剪短细线瞬间,弹簧弹力和重力不变,受力如图

由几何关系,F合=T1sinθ=T2=ma,因而a=
| T1sinθ |
| m |
| T2 |
| m |
故选B.
点评:本题为瞬时问题,关键要抓住弹簧弹力不可突变,细绳弹力可突变!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
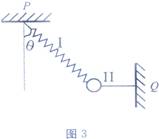
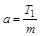 ,方向水平向左
,方向水平向左 如图所示,质量m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小T1,Ⅱ中拉力大小T2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )
如图所示,质量m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小T1,Ⅱ中拉力大小T2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )