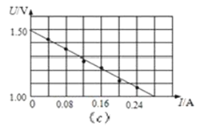
题目内容
【题目】如图,等腰梯形abcd区域内,存在垂直该平面向外的匀强磁场,ab=cd=2L,bc=L,∠bad=30°,磁感应强度大小为B,磁场外有一粒子源O,能沿同一方向发射速度大小不等的同种带电粒子,带电粒子的质量为m,电荷量为q,不计重力。现让粒子以垂直于ad的方向正对b射入磁场区域,发现带电粒子恰好都能从cd之间飞出磁场。则( )

A.粒子源发射的粒子均为带正电的粒子
B.粒子在磁场中运动的最短时间为![]()
C.带电粒子的发射速度取值范围为![]()
D.带电粒子的发射速度取值范围为![]()
【答案】AC
【解析】
A. 粒子在电场中向右偏转,根据左手定则可知,粒子带正电,故A正确;
BCD. 当粒子从c点飞出时,其运动的速度最大,轨迹所对应的圆心角最小,则运动时间最短,运动轨迹如图所示:
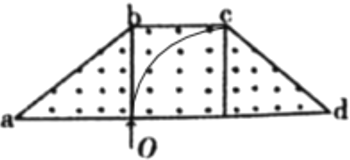
根据几何知识可知,粒子在磁场中运动的半径为:
![]()
其轨迹对应的圆心角为90°,
因为洛伦兹力提供向心力,即
![]()
所以
![]()
则粒子的速度为
![]()
粒子在磁场中运动的最短时间为:
![]()
当粒子的运动轨迹和cd相切时,粒子的速率是最小的,其运动轨迹如图所示:
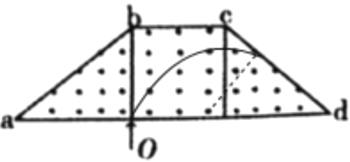
令粒子的半径为R2,根据几何知识有:
![]()
则
![]()
所以粒子的速度为:
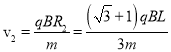
则要使粒子从cd之间射出带电粒子的发射速度取值范围为 ,故BD错误,C正确;
,故BD错误,C正确;
故选:AC。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目