题目内容
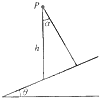如图所示，一质点位于倾角为θ的斜面上方P点，距斜面的竖直距离为h，该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上，为使质点在最短时间内从P点到达斜面，则斜面与竖直方向的夹角α应为：{积化和差公式：cosαcosβ=| 1 |
| 2 |
分析：根据牛顿第二定律求出质点的加速度，由运动学位移公式得到时间与α的关系式，根据数学知识求解时间最短时α的值．
解答：解：根据牛顿第二定律得：mgcosα=ma，得a=gcosα
质点从P点到达斜面通过的位移大小为x=
由x=
at2得，t=
联立得：t=
当α=0.5θ时，t最短，故D正确．
故选D
质点从P点到达斜面通过的位移大小为x=
| hcosθ |
| cos(θ-α) |
由x=
| 1 |
| 2 |
|
联立得：t=
|
当α=0.5θ时，t最短，故D正确．
故选D
点评：本题关键由几何知识得出位移与α的关系式，根据牛顿第二定律和运动学公式得到时间的表达式，再由数学知识求解．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图所示为一质点做匀变速直线运动的速度图象，若只研究4s前的运动情况，据图象可知（设t=0时，物体在出发点）（ ）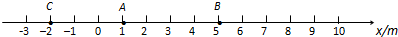
如图所示，一质点位于倾角为θ的斜面上方P点，距斜面的竖直距离为h，该质点自静止无摩檫地沿一与竖直方向夹角为α的斜槽滑至斜面上，为使质点在最短时间内从P点到达斜面，则斜面与竖直方向的夹角α应为：{积化和差公式cosαcosβ=
[cos（α+β）+cos（α-β）]}
[cos（α+β）+cos（α-β）]}（ ）