题目内容
如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下加速度与斜面倾角的关系。已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线。若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2。试问:

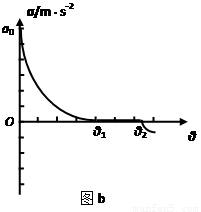
(1)图(b)中图线与纵坐标交点ao多大?
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时的摩擦力指向何方?说明在斜面倾角处于θ1和θ2之间时物块的运动状态。
(3)如果木板长L=2m,倾角为37°,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?(取sin37°=0.6,cos37°=0.8)
(1)6(m/s2) (2)处于静止状态(3)t≈3.1s
【解析】
试题分析:(1)当木板水平放置时,物块的加速度为a0
此时滑动摩擦力
f =" μN" = μmg=0.2×1×10 =" 2(N)"
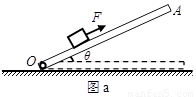
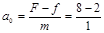 =6(m/s2)
=6(m/s2)

(2)当摩擦力沿斜面向下且加速度为零时木板倾角为θ1,当摩擦力沿斜面向上且加速度为零时木板倾角为θ2,这时物块处于静止状态。
(3) N1=mgcosθ1 F1=μN1=μmgcosθ1 F=mgsinθ1+μmgcosθ1
联立方程8 = 10sinθ1+ 2cosθ1 解得θ1≈40.4°
(4)力F作用时的加速度
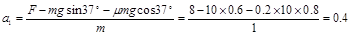 (m/s2)
(m/s2)
撤去力F后的加速度大小
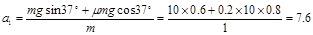 (m/s2)
(m/s2)
设物块不冲出木板顶端,力F最长作用时间为t
则撤去力F时的速度v=a1t 位移
撤去力F后运动的距离 由题意有
由题意有  即
即
 解得:t≈3.1s
解得:t≈3.1s
考点:考查力与运动的关系
点评:本题难度较小,对于涉及到摩擦力的问题时,应首先根据运动情况判断摩擦力的类型,如果给出加速度a与时间的关系图像,应用牛顿第二定律化简公式,知道图像的斜率、截距的物理意义,必要的时候根据运动学公式求解

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案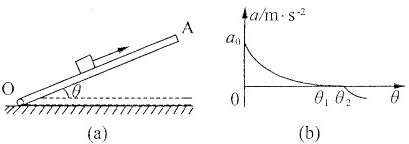
| A、由图象可知木板与水平面的夹角处于θ1和θ2之间时,物块所受摩擦力一定为零 | ||
| B、由图象可知木板与水平面的夹角大于θ2时,物块所受摩擦力一定沿木板向上 | ||
| C、根据题意可以计算得出物块加速度a0的大小为6 m/s2 | ||
D、根据题意可以计算当θ=45°时,物块所受摩擦力为f=μmgcos45°=
|
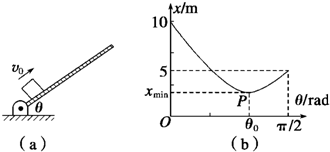 (2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:
(2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:

