题目内容
【题目】如图所示，在光滑水平面上，有一质量M=3kg的薄板，板上有质量m=1kg的物块，两者以v0=4m/S的初速度朝相反方向运动．薄板与物块之间存在摩擦且薄板足够长，求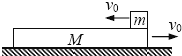
（1）当物块的速度为3m/S时，薄板的速度是多少？
（2）物块最后的速度是多少？
【答案】
（1）
由于地面光滑，物块与薄板组成的系统动量守恒，以向右为正方向，由动量守恒定律得：
Mv0﹣mv0=mv1+Mv′
代入数据解得：v′=11/3m/S，方向水平向右
（2）
在摩擦力作用下物块和薄板最后共同运动，设共同运动速度为v，以向右为正方向，由动量守恒定律得：
Mv0﹣mv0=（M+m）v
代入数据解得：v=2m/S，方向水平向右
【解析】木板与物块组成的系统动量守恒，根据木板与物块的速度，应用动量守恒定律可以求出速度．
【考点精析】掌握动量守恒定律是解答本题的根本，需要知道动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
练习册系列答案
相关题目
