题目内容
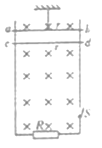
【题目】如图所示,足够长的两根光滑固定导轨相距L =0.50 m 竖直放置,导轨电阻不计,下端连接阻值为R= 1.0![]() 的电阻,导轨处于磁感应强度为B=1.0T的匀强磁场中,磁场方向垂直于导轨平面向里,两根质量均为m=0.30kg、电阻均为r=0.50
的电阻,导轨处于磁感应强度为B=1.0T的匀强磁场中,磁场方向垂直于导轨平面向里,两根质量均为m=0.30kg、电阻均为r=0.50![]() 的水平金属棒ab和cd都与导轨接触良好。金属棒ab用一根细线悬挂,现闭合开关S,让ab棒从静止开始下落,cd下落过程中,悬挂的细线恰好能够被拉断。不计空气阻力,g取10 m/s2,求:
的水平金属棒ab和cd都与导轨接触良好。金属棒ab用一根细线悬挂,现闭合开关S,让ab棒从静止开始下落,cd下落过程中,悬挂的细线恰好能够被拉断。不计空气阻力,g取10 m/s2,求:
(1)细线能承受的最大拉力Fm;
(2)细线即将被拉断时,整个电路消耗的总电功车P1;
(3)若细线被拉断时立即断开开关S,再经t=0.50 s时,cd棒的加速度为刚断开开关时加速度的4倍,求此时cd棒克服安培力做功的功率P2。
【答案】(1)5.0N;(2)30W(3)12W
【解析】(1)细线未拉断之前,当cd棒达到最大速度时,BIcdL=mg
![]()
![]() 解得:Fm=5.0N
解得:Fm=5.0N
(2)![]()
(3)细线拉断时![]()
由E=BLv0解得细线刚拉断时,cd棒的速度v0=10m/s;细线刚拉断时,开关断开,两棒的电流为![]()
cd棒的加速度![]()
细线拉断后经t=0.50s时,cd棒的加速度为![]()
由已知a2=4a1,解得I2=2A,此时感应电动势![]()
设此时两棒的速度分别为vab和vcd,有![]()
细线拉断后t=0.5s内,两棒所受安培力的冲量大小相等,设为I安,由动量定理:![]()
![]()
解得vcd=12m/s
cd棒克服安培力做功的功率:P2=BI2Lvcd=12W

练习册系列答案
相关题目