题目内容
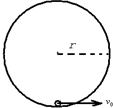宇航员在月球表面完成下面实验：在一固定的竖直光滑圆弧轨道内部的最低点，静止一质量为m的小球（可视为质点），如图所示，当给小球水平初速度V0时，刚好能使小球在竖直平面内做完整的圆周运动．已知圆弧轨道半径为r，月球的半径为R，万有引力常量为G．若在月球表面上发射一颗环月卫星，所需最小发射速度为（ ）分析：由于小球恰好经过最高点，根据重力提供向心力，可求出在最高点的速度；小球在轨道内部运动过程中，只有重力做功，由动能定理列式可求出月球表面重力加速度g，根据重力提供向心力，可求出最小发射速度．
解答：解：设月球表面重力加速度为g，月球质量为M．
球刚好完成圆周运动，则小球在最高点有 mg=m
①
从最低点至最高点由动能定理得-mg?2r=
mv2-
mv02②
由①②可得 g=
在月球表面发射卫星的最小速度为月球第一宇宙速度，重力提供向心力 m′g=m′
解得：v=
=
故选A
球刚好完成圆周运动，则小球在最高点有 mg=m
| v2 |
| r |
从最低点至最高点由动能定理得-mg?2r=
| 1 |
| 2 |
| 1 |
| 2 |
由①②可得 g=
| v02 |
| 5r |
在月球表面发射卫星的最小速度为月球第一宇宙速度，重力提供向心力 m′g=m′
| v2 |
| R |
解得：v=
| gR |
| v0 |
| 5r |
| 5Rr |
故选A
点评：本题涉及两个圆周运动，小球在光滑轨道内运动时，在最高点重力提供向心力；卫星在月球表面做圆周运动时，重力提供向心力．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
（2007?湖南模拟）宇航员在月球表面完成下面实验：在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球（可视为质点）如图所示，当施加给小球一瞬间水平冲量I时，刚好能使小球在竖直面内做完整的圆周运动．已知圆弧轨道半径为r，月球的半径为R，万有引力常量为G．
宇航员在月球表面完成下面的实验：在一固定的竖直光滑圆轨道内部有一质量为m的小球（可视为质点），如图所示．当在最高点给小球一瞬间的速度v时，刚好能使小球在竖直平面内做完整的圆周运动，已知圆弧的轨道半径为r，月球的半径为R，引力常量为G．求：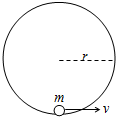
宇航员在月球表面完成下面的实验：在一固定的竖直光滑圆轨道内部最低点静止一个质量为m的小球（可视为质点），如图所示，当施给小球一瞬间速度v时，刚好能使小球在竖直平面内做完全的圆周运动，已知圆弧轨道半径为r，月球的半径为R，万有引力常量为G．求：
航天宇航员在月球表面完成了如下实验：如图所示，在月球表面固定一竖直光滑圆形轨道，在轨道内的最低点，放一可视为质点的小球，当给小球水平初速度v0时，小球刚好能在竖直面内做完整的圆周运动．已知圆形轨道半径为r，月球的半径为R．若在月球表面上发射一颗环月卫星，求最小发射速度．
宇航员在月球表面完成下面实验：在一固定的竖直光滑圆形轨道内部的最低点，静止一质量为m的小球（可视为质点），如图所示，当给小球水平初速度v0时，刚好能使小球在竖直面内做完整的圆周运动．已知圆弧轨道半径为r，月球的半径为R．若在月球表面上发射一颗环月卫星，所需最小发射速度为多大？