题目内容
(1)原子核A发生α衰变后变为原子核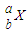 ,原子核B发生β衰变后变为原子核
,原子核B发生β衰变后变为原子核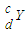 ,则原子核A的衰变方程为______b+2A→
,则原子核A的衰变方程为______b+2A→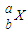 +
+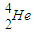
【答案】分析:(1)α衰变的过程中电荷数少2,质量数少4,β衰变的过程中电荷数多1,质量数不变.质量数等于核子数,等于中子数加上质子数.
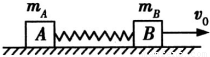
(2)两滑块与弹簧组成的系统,水平方向动量守恒,当弹簧的弹性势能最大时,两滑块损失的动能最多.
根据动量守恒和机械能守恒求解.
解答:解:(1)α衰变的过程中电荷数少2,质量数少4,β衰变的过程中电荷数多1,质量数不变,
原子核A的衰变方程为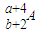 →
→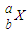 +
+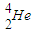
原子核B的衰变方程为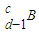 →
→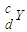 +
+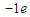
a-c=2,所以A的质量数比B的质量数大6,
若原子核A和原子核B的中子数相同,所以b-2=d-1+6
所以b-d=7.
(2)两滑块与弹簧组成的系统,水平方向动量守恒,当弹簧的弹性势能最大时,两滑块损失的动能最多.
根据动量守恒和机械能守恒得
mBv=(mB+mA)v
最大弹性势能Epm=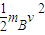 -
- (mB+mA)v2
(mB+mA)v2
解得:Epm=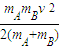
故答案为:(1)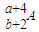 →
→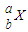 +
+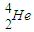 ,
,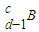 →
→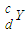 +
+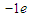 ,7
,7
(2)最大弹性势能Epm=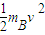 -
- (mB+mA)v2
(mB+mA)v2
点评:(1)解决本题的关键知道α衰变、β衰变的实质,知道核子数等于中子数和质子数之和.
(2)解答时注意动量守恒和机械能守恒列式分析,分析清楚物体的运动情况.
(2)两滑块与弹簧组成的系统,水平方向动量守恒,当弹簧的弹性势能最大时,两滑块损失的动能最多.
根据动量守恒和机械能守恒求解.
解答:解:(1)α衰变的过程中电荷数少2,质量数少4,β衰变的过程中电荷数多1,质量数不变,
原子核A的衰变方程为
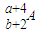 →
→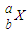 +
+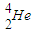
原子核B的衰变方程为
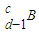 →
→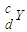 +
+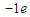
a-c=2,所以A的质量数比B的质量数大6,
若原子核A和原子核B的中子数相同,所以b-2=d-1+6
所以b-d=7.
(2)两滑块与弹簧组成的系统,水平方向动量守恒,当弹簧的弹性势能最大时,两滑块损失的动能最多.
根据动量守恒和机械能守恒得
mBv=(mB+mA)v
最大弹性势能Epm=
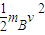 -
- (mB+mA)v2
(mB+mA)v2解得:Epm=
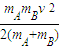
故答案为:(1)
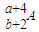 →
→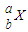 +
+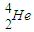 ,
,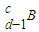 →
→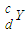 +
+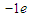 ,7
,7(2)最大弹性势能Epm=
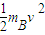 -
- (mB+mA)v2
(mB+mA)v2点评:(1)解决本题的关键知道α衰变、β衰变的实质,知道核子数等于中子数和质子数之和.
(2)解答时注意动量守恒和机械能守恒列式分析,分析清楚物体的运动情况.

练习册系列答案
相关题目
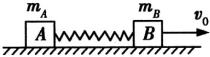 (1)原子核A发生α衰变后变为原子核
(1)原子核A发生α衰变后变为原子核