题目内容
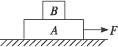
如图6所示,水平光滑地而上停放着一辆质最为M的小车,小车左端靠在竖直墙壁上,其左侧半径为R的四分之一圆弧轨道AB是光滑的,轨道最低点B与水平轨道BC相切,整个轨道处于同一竖直平面内。将质量为m的物块(可视为质点)从A点无初速释放,物块沿轨道滑行至轨道未端C处恰好没有滑出。重力加速度为g,空气阻力可忽略不计,关于物块从A位置运动至C位置的过程,下列说法中正确的是 ( )


| A.在这个过程中,小车和物块构成的系统水平方向动量守恒 |
B.在这个过程中,物块克服摩擦力所做的功为 |
C.在这个过程中,摩擦力对小车所做的功为 |
D.在这个过程中,由于摩擦生成的热量为 |
D
分析:A、系统所受合外力为零时,系统动量守恒;
B、由动能定理或机械能守恒定律求出物块滑到B点时的速度,
然后由动量守恒定律求出物块与小车的共同速度,最后由动能定理求出物块克服摩擦力所做的功;
C、由动能定理可以求出摩擦力对小车所做的功;
D、由能量守恒定律可以求出摩擦生成的热量.
解答:解:A、在物块从A位置运动到B位置过程中,小车和物块构成的系统在水平方向受到的合力不为零,系统在水平方向动量不守恒,故A错误;
B、物块从A滑到B的过程中,小车静止不动,对物块,由动能定理得:mgR=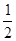 mv2-0,解得,物块到达B点时的速度
mv2-0,解得,物块到达B点时的速度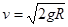 ;在物块从B运动到C过程中,物块做减速运动,小车做加速运动,最终两者速度相等,在此过程中,
;在物块从B运动到C过程中,物块做减速运动,小车做加速运动,最终两者速度相等,在此过程中,
系统在水平方向动量守恒,由动量守恒定律可得mv=(M+m)v′,v′=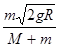 ,以物块为研究对象,
,以物块为研究对象,
由动能定理可得:-Wf=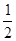 mv′2-
mv′2-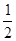 mv2,解得:Wf=mgR-
mv2,解得:Wf=mgR-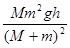 ,故B错误;
,故B错误;
C、对小车由动能定理得:Wf车=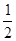 Mv′2=
Mv′2=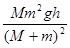 ,故C错误;
,故C错误;
D、物块与小车组成的系统,在整个过程中,由能量守恒定律得:mgR=Q+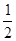 (M+m)v′2,解得:Q=
(M+m)v′2,解得:Q=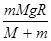 ,D项正确;
,D项正确;
故答案为:D.
点评:动量守恒条件是:系统所受合外力为零,对物体受力分析,判断系统动量是否守恒;熟练应用动量守恒定律、动能定律、能量守恒定律即可正确解题.
B、由动能定理或机械能守恒定律求出物块滑到B点时的速度,
然后由动量守恒定律求出物块与小车的共同速度,最后由动能定理求出物块克服摩擦力所做的功;
C、由动能定理可以求出摩擦力对小车所做的功;
D、由能量守恒定律可以求出摩擦生成的热量.
解答:解:A、在物块从A位置运动到B位置过程中,小车和物块构成的系统在水平方向受到的合力不为零,系统在水平方向动量不守恒,故A错误;
B、物块从A滑到B的过程中,小车静止不动,对物块,由动能定理得:mgR=
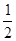 mv2-0,解得,物块到达B点时的速度
mv2-0,解得,物块到达B点时的速度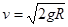 ;在物块从B运动到C过程中,物块做减速运动,小车做加速运动,最终两者速度相等,在此过程中,
;在物块从B运动到C过程中,物块做减速运动,小车做加速运动,最终两者速度相等,在此过程中,系统在水平方向动量守恒,由动量守恒定律可得mv=(M+m)v′,v′=
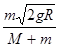 ,以物块为研究对象,
,以物块为研究对象,由动能定理可得:-Wf=
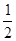 mv′2-
mv′2-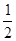 mv2,解得:Wf=mgR-
mv2,解得:Wf=mgR-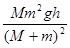 ,故B错误;
,故B错误;C、对小车由动能定理得:Wf车=
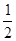 Mv′2=
Mv′2=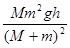 ,故C错误;
,故C错误;D、物块与小车组成的系统,在整个过程中,由能量守恒定律得:mgR=Q+
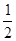 (M+m)v′2,解得:Q=
(M+m)v′2,解得:Q=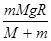 ,D项正确;
,D项正确;故答案为:D.
点评:动量守恒条件是:系统所受合外力为零,对物体受力分析,判断系统动量是否守恒;熟练应用动量守恒定律、动能定律、能量守恒定律即可正确解题.

练习册系列答案
相关题目
 射线强,能穿透几厘米厚的铅板
射线强,能穿透几厘米厚的铅板
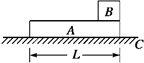
 =0.5,A、B、C均可视为质点,重力加速度为g.
=0.5,A、B、C均可视为质点,重力加速度为g. 一段时间A与C相碰,设碰撞时间极短,碰后一起压缩弹簧,弹簧最大压缩量为
一段时间A与C相碰,设碰撞时间极短,碰后一起压缩弹簧,弹簧最大压缩量为 L,求弹簧的最大弹性势能。
L,求弹簧的最大弹性势能。
 的小球被长为L的轻质细绳悬挂,小球可以绕悬点O在竖直平面内摆动,不计空气阻力,则开始小球静止且恰能与地面接触而不发生相互作用,一个质量为
的小球被长为L的轻质细绳悬挂,小球可以绕悬点O在竖直平面内摆动,不计空气阻力,则开始小球静止且恰能与地面接触而不发生相互作用,一个质量为 的小物块在光滑水平面上滑行并与小球发生正碰,碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动,当小球再次与物块发生正碰后,小物块速度变为最初速度的一半,已知重力加速度为
的小物块在光滑水平面上滑行并与小球发生正碰,碰后物块静止不动而小球在竖直平面内刚好可以通过最高点做圆周运动,当小球再次与物块发生正碰后,小物块速度变为最初速度的一半,已知重力加速度为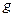 ,两物体均可视为质点,试求
,两物体均可视为质点,试求
 。
。