题目内容
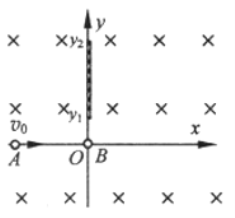
【题目】如图所示,整个空间有一垂直于直角坐标系xOy平面向里的足够大的匀强磁场,在y轴上从![]() 到
到![]() 之间有一厚度不计的固定弹性绝缘板。在x轴负半轴上某一位置有一个质量为m的不带电粒子A,以一定速率
之间有一厚度不计的固定弹性绝缘板。在x轴负半轴上某一位置有一个质量为m的不带电粒子A,以一定速率![]() 沿x轴向正方向运动,并与在原点O处静止的另一个质量为3m、所带电荷量为q的带正电的粒子B发生碰撞并粘在一起,形成新粒子C。已知碰撞时没有质量和电荷量损失,粒子均可视为质点,且所有粒子不计重力。
沿x轴向正方向运动,并与在原点O处静止的另一个质量为3m、所带电荷量为q的带正电的粒子B发生碰撞并粘在一起,形成新粒子C。已知碰撞时没有质量和电荷量损失,粒子均可视为质点,且所有粒子不计重力。
(1)求A、B粒子碰撞过程中系统损失的动能;
(2)如果让C粒子能够打到绝缘板上,求匀强磁场磁感应强度应满足的条件;
(3)C粒子先与绝缘板碰撞两次后经过坐标为![]() 、
、![]() 的位置P(图中未画出),已知C粒子与弹性绝缘板碰撞没有能量和电荷量损失,求匀强磁场磁感应强度的大小。
的位置P(图中未画出),已知C粒子与弹性绝缘板碰撞没有能量和电荷量损失,求匀强磁场磁感应强度的大小。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1) A、B粒子碰撞过程中由动量守恒定律
![]()
解得
![]()
系统损失的动能
![]()
(2)若使粒子打到绝缘板上的最下端,则
![]()
由
![]()
解得
![]()
若使粒子打到绝缘板上的最上端,则
![]()
由
![]()
解得
![]()
则如果让C粒子能够打到绝缘板上,匀强磁场磁感应强度应满足的条件是
![]()
(3) C粒子先与绝缘板碰撞两次后经过坐标为![]() 、
、![]() 的位置P,则运动轨迹如图
的位置P,则运动轨迹如图

此时粒子C的轨道半径为r,则由几何关系可知
![]()
则解得
r=L0
或者
![]()
![]()
解得
![]()
或者
![]()

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目