题目内容
12．
一半径为R的绝缘光滑的圆环竖直放置在水平向右的场强为E的匀强电场中，如图，环上a、c是竖直直径的两端，b、d是水平直径的两端，质量m的带电小球套在圆环上，并可沿环无摩擦滑动，已知小球从a点由静止释放，沿abc运动到d点时速度恰好为0，由此可知（ ）| A． | 小球在c点时动能最大 | |
| B． | 小球在b、c点间某位置获得最大动能 | |
| C． | 小球在d点时电势能最大 | |
| D． | 小球在b点时电势能最大 |
分析 小球由a点释放，受到重力、电场力和环的弹力作用，根据电场力做功与电势能变化的关系得到电势能的变化情况，根据动能定理判断动能的变化情况，由向心加速度公式an=$\frac{{v}^{2}}{r}$分析向心加速度，根据除重力外其余力做功判断机械能的变化情况．
解答 解：A、由题，小球从a点由静止释放，沿abc运动到d点时速度恰好为0，可知小球带负电，当小球的速度最大上，小球位于等效最低点处，该处一定位于c与b之间．故A错误，B正确；
C、小球带负电，所以在电势最低的点d，小球的电势能最大．故C正确，D错误．
故选：BC
点评 该题属于等效场中竖直平面内的圆周运动，解答本题关键是对小球受力分析后，正确判断出等效最低点，然后能够灵活地运用功能关系列式分析求解．
练习册系列答案
相关题目
2．火星是太阳系中地球外侧离地球最近的行星，当地球在火星和太阳之间且成一条直线时，称为行星冲日现象，已知地球的公转周期为1年，火星的公转周期约为地球的两倍，则火星和地球相邻两次冲日的时间间隔大约为（ ）
| A． | 1年 | B． | 2年 | C． | 4年 | D． | 8年 |
3．电子绕核运动可以看做一环形电流．设氢原子中的电子绕原子核在半径为r的轨道上运动，用e表示电荷量，m表示电子的质量，K为静电力常量．则（ ）
| A． | 电子运动的速率为$v=e\sqrt{\frac{k}{mr}}$ | B． | 电子运动的周期为$T=\frac{2πr}{e}\sqrt{\frac{m}{k}}$ | ||
| C． | 电子运动形成的电流$I=\frac{e^2}{2πr}\sqrt{\frac{k}{mr}}$ | D． | 电子运动形成的电流$I=\frac{{{e^{\;}}}}{2πr}\sqrt{\frac{k}{mr}}$ |
20．一物体在水平面上以恒定加速度运动，位移与时间的关系x=24t─6t2，则其速度为零的时刻是（ ）
| A． | 4s末 | B． | 2s末 | C． | 6s末 | D． | 24s末 |
7．升降机底板上放一质量为10kg的物体，物体随升降机由静止开始竖直上升6m时，速度达到10m/s，则此过程中（重力加速度g取10m/s2）（ ）
| A． | 合外力对物体做功600 J | B． | 物体的重力势能增加600 J | ||
| C． | 升降机对物体做功500 J | D． | 物体的机械能增加1100 J |
17．
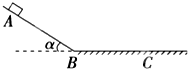如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据，请充分利用这些数据，求：（重力加速度g=10m/s2 ）
（1）物体在AB段和在BC段的加速度a1和a2的大小；
（2）物体运动到B点所用时间t1及达到B点的速率VB．
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据，请充分利用这些数据，求：（重力加速度g=10m/s2 ）| t（s） | 0.0 | 0.2 | 0.4 | … | 1.2 | 1.4 | … |
| v（m/s） | 0.0 | 1.0 | 2.0 | … | 1.1 | 0.7 | … |
（2）物体运动到B点所用时间t1及达到B点的速率VB．
4．汽车以6m/s的速度在平直的公路上匀速行驶，紧急刹车时以大小2m/s2的加速度在粗糙的公路上滑行，则在刹车后2s和4s内汽车的位移分别为（ ）
| A． | 8m和8m | B． | 8m和9m | C． | 16m和40m | D． | 12m和24m． |
如图所示为简单欧姆表原理示意图，其中电流表的满偏电流Ig=100μA，内阻Rg=100Ω，可变电阻R的最大阻值为10kΩ，电池的电动势E=1.5V，内阻r=0.5Ω，图中与接线柱B相连的表笔颜色应是黑色．按正确使用方法测量电阻Rx的阻值时，指针指在刻度盘的正中央，则Rx=15kΩ．