题目内容
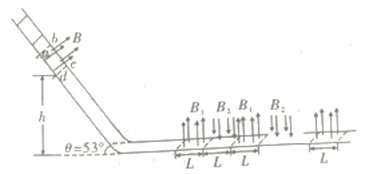
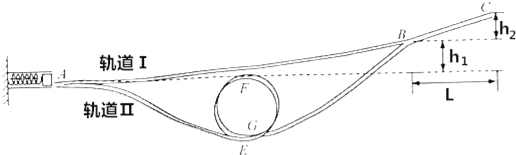
【题目】如图所示，装置由一理想弹簧发射器及两个轨道组成．其中轨道Ⅰ由光滑轨道AB与粗糙直轨道BC平滑连接，高度差分别是h1=0.2m、h2=0.10m，BC水平距离L=1.00m．轨道Ⅱ由AE、螺旋圆形EFG和GB三段光滑轨道平滑连接而成，且A点与F点等高．当弹簧压缩量为d时，恰能使质量m=0.05kg的滑块沿轨道Ⅰ上升到B点；当弹簧压缩量为2d时，恰能使滑块沿轨道Ⅰ上升到C点．（已知弹簧弹性势能与压缩量的平方成正比）
（1）当弹簧压缩量为d时，求弹簧的弹性势能及滑块离开弹簧瞬间的速度大小；
（2）求滑块与轨道BC间的动摩擦因数；
（3）当弹簧压缩量为d时，若沿轨道Ⅱ运动，滑块能否上升到B点？请通过计算说明理由．
【答案】（1）0.1J 2m/s (2)0.5 (3)不能到达B点
【解析】
试题当弹簧压缩量为d时，释放后弹簧的弹性势能转化为滑块的动能，滑块在轨道Ⅰ上升到B点的过程中，滑块的动能转化为重力势能，由机械能守恒定律求解．当弹簧压缩量为2d时，弹簧的弹性势能是弹簧压缩量为d时弹性势能的4倍，对滑块释放到C的整个过程，运用能量守恒定律列式，可求得滑块与轨道BC间的动摩擦因数．若要能使滑块上升到B点，根据机械能守恒定律分析能否上升到B点。
(1)由机械能守恒定律可得
E弹＝ΔEk＝ΔEp＝mgh1＝0.05×10×0.20 J＝0.1 J
根据：
可解得：v0＝2 m/s
(2) 当弹簧压缩量为2d时，由题可得：弹簧的弹性势能是弹簧压缩量为d时弹性势能的4倍，即为：EP2=4EP1=0.4J
对滑块从弹簧释放后运动到C点的过程，根据能量守恒定律得：
解得：μ=0.5
(3)恰能通过螺旋轨道最高点须满足的条件是：
由机械能守恒定律有：
解得：v＝v0＝2 m/s
得Rm＝0.4m
当R≤Rm＝0.4m时，滑块能够上升到B点．
当R>Rm＝0.4m时，滑块会脱离螺旋轨道，不能上升到B点。
