题目内容
（15分）如图，足够长的斜面倾角θ＝37°，一物体以v0＝12m/s的初速度，从斜面A点沿斜面向上运动，加速度大小为a＝8.0m／s2．已知重力加速度g=10m/s2，sin 37°= 0.6，cos 37°= 0.8．求：
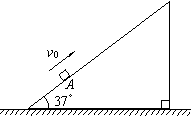
（1）物体沿斜面上滑的最大距离s；
（2）物体与斜面间的动摩擦因数μ；
（3）物体沿斜面到达最高点后返回下滑至A点时的速度大小v。
解析：
（1）根据运动学公式 2as ＝ v （2分）
解得 
（1分）
（2）根据牛顿第二定律 mg sin 37°＋ μmg cos 37°＝ ma （4分）
解得 
（2分）
（3）设沿斜面下滑时的加速度为a′，根据牛顿第二定律
mg sin 37°－ μmg cos 37°＝ ma′
解得 a′＝ g sin 37°－ μg cos 37°＝ g （sin 37°－ μ cos 37°） （3分）
＝10×（0.6－0.8×
）＝ 4 （m／s2） （1分）
根据运动学公式 2a′s ＝ v2
解得 v＝
（2分）
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，足够长的斜面倾角θ=30°，一个物体以12m/s的初速度从面上点处沿斜面向上运动，加速度大小为a=8.0m/s2 （g=10m/s2），求：
如图，足够长的斜面倾角θ=37°．一个物体以v0=12m/s的初速度从斜面A点处沿斜面向上运动．物体与斜面间的动摩擦因数为μ=0.25．已知重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．求：