题目内容
10. 如图所示,质量为m的物块与转台之间能出现的最大静摩擦力为物块重力的k倍.它与转轴OO′相距R,物块随转台由静止开始转动,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到开始滑动前的这一过程中,转台对物块做的功为$\frac{1}{2}kmgR$.
如图所示,质量为m的物块与转台之间能出现的最大静摩擦力为物块重力的k倍.它与转轴OO′相距R,物块随转台由静止开始转动,当转速增加到一定值时,物块即将在转台上滑动,在物块由静止到开始滑动前的这一过程中,转台对物块做的功为$\frac{1}{2}kmgR$.
分析 根据最大静摩擦力求出物块刚好发生转动时的线速度大小,结合动能定理求出转台做功的大小.
解答 解:根据牛顿第二定律得,$kmg=m\frac{{v}^{2}}{R}$,
根据动能定理得,W=$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}kmgR$
故答案为:$\frac{1}{2}kmgR$.
点评 本题考查了动能定理和牛顿第二定律的基本运用,通过最大静摩擦力求出发生滑动时的速度是解决本题的关键.

练习册系列答案
相关题目
1.小青同学利用细线和橡皮塞做感受向心力的实验.A、B为细绳上打的两个结点,橡皮塞在水平面内做匀速圆周运动,如图乙所示.如果忽略空气阻力的影响,则以下说法中错误的是( )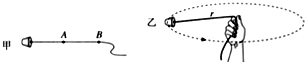
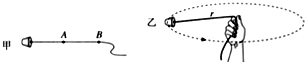
| A. | A、B两点的角速度相同 | B. | A、B两点的运动周期相同 | ||
| C. | 橡皮塞受重力和拉力的作用 | D. | 橡皮塞所受拉力沿水平方向 |
18.在“探究功与速度变化的关系”实验中,某同学所用的实验装置如图所示.关于这一实验,下列说法正确的是( )
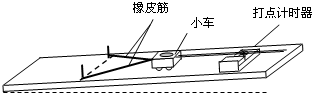

| A. | 长木板要适当倾斜,以平衡小车运动中受到的阻力 | |
| B. | 重复实验时,虽然用到橡皮筋的条数不同,但每次应使橡皮筋拉伸的长度相同 | |
| C. | 利用纸带上的点计算小车的速度时,应选用纸带上打点最密集的部分进行计算 | |
| D. | 利用纸带上的点计算小车的速度时,应选用纸带上打点间距均匀部分进行计算 |
5.物体在运动过程中克服重力做功为100J,则下列说法中正确的是( )
| A. | 物体的重力势能一定增加了100 J | B. | 物体的重力势能一定减少了100 J | ||
| C. | 物体的动能一定增加了100 J | D. | 物体的动能一定减少了100 J |

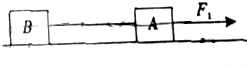 如图所示,放置于水平面物体A、B相距L=19m,中间用绷紧的水平细绳相连,已知A的质量mA=10kg,B的质量mB=5kg,A、B与水平面的动摩擦因数μ=0.2,某时刻用F1=90N的力水平作用在A上,使A、B一起向右运动,经过t1=2.5s后撤去力F1,同时使A停下来.再经过时间t2用与F1方向相同,大小为60N的力F2作用于A上.求
如图所示,放置于水平面物体A、B相距L=19m,中间用绷紧的水平细绳相连,已知A的质量mA=10kg,B的质量mB=5kg,A、B与水平面的动摩擦因数μ=0.2,某时刻用F1=90N的力水平作用在A上,使A、B一起向右运动,经过t1=2.5s后撤去力F1,同时使A停下来.再经过时间t2用与F1方向相同,大小为60N的力F2作用于A上.求