题目内容
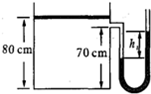（2009?嘉定区二模）一足够高的直立气缸上端开口，用一个厚度不计的活塞封闭了一段高为80cm的气柱，活塞的横截面积为0.01m2，活塞与气缸间的摩擦不计．气缸侧壁通过一个开口与U形管相连，开口离气缸底部的高度为70cm，开口管内及U形管内的气体体积忽略不计．已知图所示状态时，气体的温度为7 0C，U形管内水银面的高度差h1=5cm．大气压强p0=1.0×105 Pa保持不变．水银的密度ρ=13.6×103 kg/m3．求：（1）活塞的重力．
（2）现在活塞上添加沙粒，同时对气缸内的气体加热，始终保持活塞的高度不变，此过程缓慢进行，当气体的温度升高到37℃时，U形管内水银的高度差为多少？
（3）保持上题中的沙粒质量不变，让气缸内的气体逐渐冷却，那么当气体的温度至少降为多少时，U形管内的水银面变为一样高？
分析：（1）封闭气体的压强可以以活塞为研究对象求出，也可以根据水银柱求出，即封闭气体的压强P=P0+
，又有P=P0+ρgh1，联立解得活塞的重力．
（2）活塞的高度不变，U形管内的气体体积忽略不计，则气缸内气体发生等容变化，根据查理定律求解U形管内水银的高度差．
（3）U形管内的水银面变为一样高时，则知U形管内的两臂均与大气相通，此前气体做等压变化，根据盖?吕萨克定律求解温度．
| G活 |
| S |
（2）活塞的高度不变，U形管内的气体体积忽略不计，则气缸内气体发生等容变化，根据查理定律求解U形管内水银的高度差．
（3）U形管内的水银面变为一样高时，则知U形管内的两臂均与大气相通，此前气体做等压变化，根据盖?吕萨克定律求解温度．
解答：解：（1）由P0+
=P0+ρgh1，得G活=ρgh1S=ρ=13.6×103×10×0.05×0.01N=68N
（2）因为活塞的位置保持不变，U形管内的气体体积忽略不计，所以气缸内气体近似做等容变化，则有
=
解得，h2=0.134m
（3）当U形管内的水银面变为一样高时，则知U形管内的两臂均与大气相通，此前气体做等压变化，根据盖?吕萨克定律得
=
代入得
=
解得，t3=-1.75℃
答：（1）活塞的重力是68N．
（2）当气体的温度升高到37℃时，U形管内水银的高度差为0.134m．
（3）当气体的温度至少降为-1.75℃时，U形管内的水银面变为一样高．
| G活 |
| S |
（2）因为活塞的位置保持不变，U形管内的气体体积忽略不计，所以气缸内气体近似做等容变化，则有
| P0+ρgh1 |
| T1 |
| P0+ρgh2 |
| T2 |
解得，h2=0.134m
（3）当U形管内的水银面变为一样高时，则知U形管内的两臂均与大气相通，此前气体做等压变化，根据盖?吕萨克定律得
| V1 |
| T1 |
| V2 |
| T3 |
代入得
| 80 |
| 273+37 |
| 70 |
| 273+t3 |
解得，t3=-1.75℃
答：（1）活塞的重力是68N．
（2）当气体的温度升高到37℃时，U形管内水银的高度差为0.134m．
（3）当气体的温度至少降为-1.75℃时，U形管内的水银面变为一样高．
点评：本题是气体问题，确定气体状态作何种变化是关键，要充分挖掘隐含的条件进行分析．
练习册系列答案
相关题目
（2009?嘉定区二模）小灯泡通电后其电流I随所加电压U变化的图线如图所示，P为图线上一点，PN为图线的切线，PQ为U轴的垂线，PM为I轴的垂线．则下列说法中正确的是（ ）
（2009?嘉定区二模）（单选）如图所示的实验装置中，把浸有乙醚的一小块棉花放在厚玻璃筒内底部，当很快向下压活塞时，由于被压缩的气体骤然变热，温度升高达到乙醚的燃点，使浸有乙醚的棉花燃烧起来，此实验的目的是要说明对物体（ ）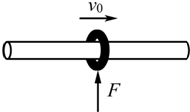
（2009?嘉定区二模）如图所示，一个质量为m的圆环套在一根固定的水平长直杆上，环与杆间的动摩擦因数为μ．现给环一个向右的初速度v0，同时对环施加一个竖直向上的作用力F，并使F的大小随v的大小变化，两者关系为F=kv，其中k为常数，则环在运动过程中克服摩擦所做的功大小可能为（ ）
（2009?嘉定区二模）如图所示，一支两端封闭的玻璃管ab倾斜放置，与水平面的夹角为θ，正中有一段水银柱，两端各封闭有一定质量的理想气体，下列情况中能使水银柱向b端移动的是（ ）