题目内容
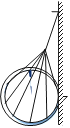
【题目】如图所示，竖直平面内轨道ABCD的质量M=0.4kg，放在光滑水平面上，其中AB段是半径为R=0.4m的光滑四分之一圆弧，在B点与水平轨道BD相切，水平轨道的BC段粗糙，动摩擦因数μ=0.4，长L=3.5m，CD段光滑，D端连一轻弹簧，现有一质量m=0.1kg的小物体（可视为质点）在距A点高为H=3.6m处由静止自由落下，恰沿A点滑入圆弧轨道（
），求：
（ⅰ）ABCD轨道在水平面上运动的最大速率；
（ⅱ）小物体第一次演轨道返回A点时的速度大小。
【答案】①
②
【解析】试题分析：①由题意分析可知，当小物体沿运动到圆弧最低点B时轨道的速率最大，设为vm，假设此时小物体的速度大小为v，则小物体和轨道组成的系统水平方向动量守恒：以初速度的方向为正方向；由动量守恒定律可得： 
，由机械能守恒得： 
，联立并代入数据解得： 
②由题意分析可知，小物体第一次沿轨道返回到A点时小物体与轨道在水平方向的分速度相同，设为
，假设此时小物体在竖直方向的分速度为
，则对小物体和轨道组成的系统，由水平方向动量守恒得： 
由能量守恒得： 
联立并代入数据解得： 
；
故小物体第一次沿轨道返回到A点时的速度大小为： 
练习册系列答案
相关题目
