题目内容
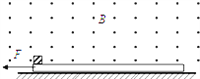
【题目】如图所示，质量相同的两小球a、b分别从斜面顶端A和斜面中点B沿水平方向抛出后，恰好都落在斜面底端，不计空气阻力，下列说法正确的是
A. 小球a、b在空中飞行的时间之比为4: 1
B. 小球a、b抛出时的初速度大小之比为2: 1
C. 小球a、b到达斜面底端时的速率之比为
: 1
D. 小球a、b到达斜面底端时速度方向与斜面的夹角之比为1:1
【答案】CD
【解析】试题分析：根据下降的高度之比，结合位移时间公式求出小球a、b在空中飞行的时间之比，根据水平位移之比和时间之比求出初速度之比．平抛运动速度方向与水平方向夹角的正切值是位移方向与水平方向夹角正切值的2倍，结合该推论分析小球到达底端时速度方向与斜面夹角的关系．
两球下落的高度之比为2：1，根据
知，
，则飞行的时间之比为
，A错误．两球的水平位移之比为2：1，飞行时间之比为，根据
知，两球的初速度之比为，B错误；根据动能定理可知达斜面底端时
，即
知
，C正确；小球落在斜面上，速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍，因为位移与水平方向的夹角相等，则速度与水平方向的夹角相等，到达斜面底端时速度方向与斜面的夹角也相等，故D正确．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
