Question

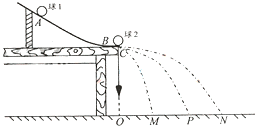
如图19所示装置由AB、BC、CD三段轨道组成，轨道交接处均由很小的圆弧平滑连接，其中轨道AB、CD段是光滑的，水平轨道BC的长度x=5m，轨道CD足够长且倾角θ=37^o，A、D两点离轨道BC的高度分别为h1=4．30m, h2=1．35m，现让质量为m的小滑块自A点由静止释放，已知小滑块与轨道BC间的动摩擦因数为μ=0．5，重力加速度g取10m/s²，sin37^o=0．6，cos37^o=0．8，求：

（1）小滑块第一次到达D点时的速度大小

（2）小滑块第一次与第二次通过C点的时间间隔

（3）小滑块最终停止的位置距B点的距离

 

Answer 1

解析：

（1）小滑块从A经过B、C运动到D的过程，由动能定理得：

         …………………．……．．3分

代入数据解得：          …………………．……．．1分

（2）小滑块从A经过B运动到C的过程，由动能定理得：

，            …………………．……．．1分

代入数据解得：          …………………．……．．1分

小滑块沿CD段上滑的加速度大小

小滑块沿CD段上滑到最高点的时间,………………．．1分

由对称性可知，小滑块从最高点滑回C点的时间，

故小滑块第一次与第二次通过C点的时间间隔。……．．1分

（注：用动量定理求解时间同样得分）

（3）对小滑块运动的全过程利用动能定理，设小滑块在水平轨道上运动的总路程为s，

，           …………………．……．．2分

代入数据解得：                …………………．……．．1分

故小滑块最终停止的位置距B点的距离为：………．．1分