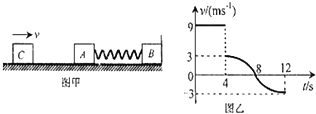
题目内容
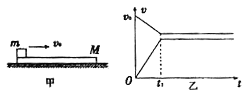
【题目】如图所示,质量为m的物体(可视为质点)以水平速度V0滑上原来静止在光滑水平面上质量为M的小车上,物体与小车的动摩擦因数为![]() ,小车足够长,求:
,小车足够长,求:
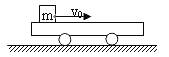
(1)最终m与M的共同速度为多大?
(2)物体从滑上小车到相对小车静止所经历的时间?
(3)物体相对小车滑行的距离?
(4)到物体相对小车静止时,小车通过的距离。
【答案】 (1) ![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4) 
【解析】物块滑上小车后,受到向左的滑动摩擦力而做减速运动,小车受到向右的滑动摩擦力而做加速运动,因小车足够长,最终物块与小车相对静止,由于水平面光滑,系统所受合外力为零,故满足动量守恒定律.
(1)取向右为正方向,设最终m与M的共同速度为v.由动量守恒定律,得:
mv0=(M+m)v
解得 ![]()
(2)对m,由动量定理:-μmgt=mv-mv0
可以解得: ![]()
(3)由功能关系,系统克服摩擦力做功等于系统机械能的减少量,即:
μmg△x=![]() mv02-
mv02-![]() (M+m)v2;
(M+m)v2;
解得,物体相对小车滑行的距离![]()
(4)对小车,由动能定理得:μmgs=![]() Mv2;
Mv2;
则得: ![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目