题目内容
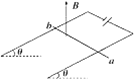
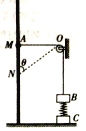
【题目】如图所示,固定竖直绝缘长杆上套有圆环A,竖直轻弹簧两端分别固定有质量均为m的物块B和C,用一根不可伸长的柔软轻质绝缘细绳绕过小定滑轮O系着A和B,杆上M点与0等高。开始时A在M点,此时滑轮两侧的轻绳伸直且无张力;当A放置在N点时系统平衡,恰好要高开水平地面,此时轻绳与杆的夹角θ=53°.已知重力加速度大小为g,取sin53°=0.8,os53°=0.6.弹簧的劲度系数为k,弹簧始终处在弹性限度内,A、B和C均可视为质点,不计一切摩擦。
(1)求A的质量![]() ;
;
(2)若将A从M点由静止释放,求A沿杆下清过程中的最大速度;
(3)若A带电B和C均不带电,且将整个装置放在整直方向的匀强电场中,已知A受到的电场力大小是A所受重力大小的2倍,但方向未知,A仍从M点由静止释放,请讨论并求C恰好要离开水平地面时A的速度大小。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)A放置在N点系统平衡时,对B、C整体有:T=2mg
对A有Tcos53°=m0g
解得:m0=5m/6
(2)A在M点时,对B有:kx1=mg
A过N点时的速度最大,此时对C有:kx2=mg
解得:x1=x2=mg/k
由于x1=x2,故A在M点和在N点时弹簧弹性势能相等,在A 从M点下滑到N 点的过程中,对A、B、C
及弹簧组成的系统,由机械能守恒定律有:
![]()
由几何关系可知: ![]() ,
, ![]()
将A过N点时的速度沿轻绳和垂直轻绳方向分解,有: ![]()
解得: ![]()
(3)A受到的电场力大小F=2m0g
若A受到的电场力方向竖直向上,则A将沿杆向上运动,等效重力为:
![]()
根据对称性,C要离开水平地面时,A运动到M点上方距离为h 的N′点.且A的速度大小为: ![]()
若A受到的电场力方向竖直向下,则A将沿杆向下运动,根据动能定理有:
![]()
将A过N点时的速度沿轻绳和垂直轻绳方向分解,有: ![]()
解得: ![]() =
=![]()