题目内容
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,请说明所加磁场的方向.
(2)如M、N极板间的电场强度为E、垂直纸面的匀强磁场的磁感应强度B,K与A间的电压为U,电子恰能沿直KO穿过平行金属板,打在荧光屏正中央,求电子的比荷(电荷量和质量之比)
(3)已M、N板的长度L1,两极板右端到荧光屏的距离L2,如果保M、N极板间的电场强E,以及加速电U不变,而撤去所加的磁场,求电子打到荧光屏上的位置O点的距离.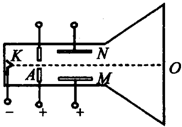
(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,请说明所加磁场的方向.
(2)如M、N极板间的电场强度为E、垂直纸面的匀强磁场的磁感应强度B,K与A间的电压为U,电子恰能沿直KO穿过平行金属板,打在荧光屏正中央,求电子的比荷(电荷量和质量之比)
(3)已M、N板的长度L1,两极板右端到荧光屏的距离L2,如果保M、N极板间的电场强E,以及加速电U不变,而撤去所加的磁场,求电子打到荧光屏上的位置O点的距离.

(1)电子通过M、N极板间电场、磁场区域时不发生偏转,电子,所受的电场力与洛伦兹力大小相等、方向相反,电子所受的电场力竖直向下,则洛伦兹力竖直向上,由左手定则可判定磁场方向磁场垂直纸面向外.
(2)电子穿过M、N极板间时受力平衡,则有:eE=ev0B,
电子在KA间经电压U加速时有:eU=
m
联立解得,电子的比荷为:
=
(3)撤去所加的磁场后,电子通过M、N两板间时,做类平抛运动,在竖直方向做初速度为零的匀加速直线运动,水平方向做匀速直线运动.
电子在MN间运动的时间为:t1=
,加速度为:a=
则电子的偏转距离为:y1=
a
=
=
电子离开MN间电场后做匀速直线运动,到达荧光屏的时间为:t2=
,电子竖直方向的分速度为:vy=at1=
,电子在竖直方向上位移大小为:
y2=vyt2=
=
故电子打到荧光屏上的位置O点的距离为:Y=y1+y2=
答:(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,所加磁场的方向垂直纸面向外.
(2)电子的比荷为
.
(3)电子打到荧光屏上的位置O点的距离为
.
(2)电子穿过M、N极板间时受力平衡,则有:eE=ev0B,
电子在KA间经电压U加速时有:eU=
| 1 |
| 2 |
| v | 20 |
联立解得,电子的比荷为:
| e |
| m |
| E2 |
| 2UB2 |
(3)撤去所加的磁场后,电子通过M、N两板间时,做类平抛运动,在竖直方向做初速度为零的匀加速直线运动,水平方向做匀速直线运动.
电子在MN间运动的时间为:t1=
| L1 |
| v0 |
| eE |
| m |
则电子的偏转距离为:y1=
| 1 |
| 2 |
| t | 21 |
eE
| ||
2m
|
E
| ||
| 4U |
电子离开MN间电场后做匀速直线运动,到达荧光屏的时间为:t2=
| L2 |
| v0 |
| eEL1 |
| mv0 |
y2=vyt2=
| eEL1L2 | ||
m
|
| EL1L2 |
| 2U |
故电子打到荧光屏上的位置O点的距离为:Y=y1+y2=
| EL1(L1+2L2) |
| 4U |
答:(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,所加磁场的方向垂直纸面向外.
(2)电子的比荷为
| E2 |
| 2UB2 |
(3)电子打到荧光屏上的位置O点的距离为
| EL1(L1+2L2) |
| 4U |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
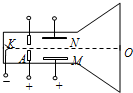 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
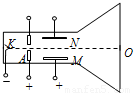 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.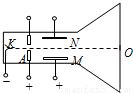 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.