题目内容
 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,请说明所加磁场的方向.
(2)如M、N极板间的电场强度为E、垂直纸面的匀强磁场的磁感应强度B,K与A间的电压为U,电子恰能沿直KO穿过平行金属板,打在荧光屏正中央,求电子的比荷(电荷量和质量之比)
(3)已M、N板的长度L1,两极板右端到荧光屏的距离L2,如果保M、N极板间的电场强E,以及加速电U不变,而撤去所加的磁场,求电子打到荧光屏上的位置O点的距离.
【答案】分析:(1)为使电子M、N极板间不发生偏转,必须使电子所受的电场力与洛伦兹力大小相等、方向相反,由左手定则可判断磁场方向.
(2)电子恰能沿直KO穿过平行金属板时,在MN间时,受力平衡,由平衡条件得出速度与场强的关系,在KA间加速时,由动能定理求出电子获得的速度,联立求解电子的比荷.
(3)电子通过M、N两板间时,做类平抛运动,运用运动的分解,由牛顿第二定律和运动学公式求出偏转的距离和竖直方向上的分速度.电子离开MN间电场后做匀速直线运动,由位移公式求出竖直方向的位移.即可得解.
解答:解:(1)电子通过M、N极板间电场、磁场区域时不发生偏转,电子,所受的电场力与洛伦兹力大小相等、方向相反,电子所受的电场力竖直向下,则洛伦兹力竖直向上,由左手定则可判定磁场方向磁场垂直纸面向外.
(2)电子穿过M、N极板间时受力平衡,则有:eE=evB,
电子在KA间经电压U加速时有:eU=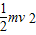
联立解得,电子的比荷为: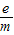 =
=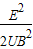
(3)撤去所加的磁场后,电子通过M、N两板间时,做类平抛运动,在竖直方向做初速度为零的匀加速直线运动,水平方向做匀速直线运动.
电子在MN间运动的时间为:t1=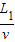 ,加速度为:a=
,加速度为:a=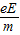
则电子的偏转距离为:y1=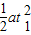 =
=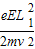 =
=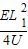
电子离开MN间电场后做匀速直线运动,到达荧光屏的时间为:t2=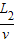 ,电子竖直方向的分速度为:vy=at1=
,电子竖直方向的分速度为:vy=at1=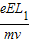 ,电子在竖直方向上位移大小为:
,电子在竖直方向上位移大小为:
y2=vyt2=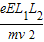 =
=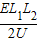
故电子打到荧光屏上的位置O点的距离为:Y=y1+y2=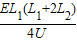
答:(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,所加磁场的方向垂直纸面向外.
(2)电子的比荷为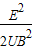 .
.
(3)电子打到荧光屏上的位置O点的距离为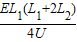 .
.
点评:本题是电场加速、偏转及速度选择器的组合.按程序法进行分析研究,偏转问题,运用运动的分解处理,电子离开电场后也运用分解法研究.
(2)电子恰能沿直KO穿过平行金属板时,在MN间时,受力平衡,由平衡条件得出速度与场强的关系,在KA间加速时,由动能定理求出电子获得的速度,联立求解电子的比荷.
(3)电子通过M、N两板间时,做类平抛运动,运用运动的分解,由牛顿第二定律和运动学公式求出偏转的距离和竖直方向上的分速度.电子离开MN间电场后做匀速直线运动,由位移公式求出竖直方向的位移.即可得解.
解答:解:(1)电子通过M、N极板间电场、磁场区域时不发生偏转,电子,所受的电场力与洛伦兹力大小相等、方向相反,电子所受的电场力竖直向下,则洛伦兹力竖直向上,由左手定则可判定磁场方向磁场垂直纸面向外.
(2)电子穿过M、N极板间时受力平衡,则有:eE=evB,
电子在KA间经电压U加速时有:eU=
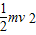
联立解得,电子的比荷为:
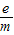 =
=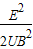
(3)撤去所加的磁场后,电子通过M、N两板间时,做类平抛运动,在竖直方向做初速度为零的匀加速直线运动,水平方向做匀速直线运动.
电子在MN间运动的时间为:t1=
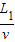 ,加速度为:a=
,加速度为:a=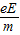
则电子的偏转距离为:y1=
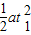 =
=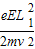 =
=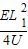
电子离开MN间电场后做匀速直线运动,到达荧光屏的时间为:t2=
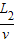 ,电子竖直方向的分速度为:vy=at1=
,电子竖直方向的分速度为:vy=at1=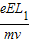 ,电子在竖直方向上位移大小为:
,电子在竖直方向上位移大小为:y2=vyt2=
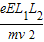 =
=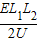
故电子打到荧光屏上的位置O点的距离为:Y=y1+y2=
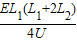
答:(1)为使电子M、N极板间不发生偏转,需在M、N极板间加一个垂直纸面的匀强磁场,所加磁场的方向垂直纸面向外.
(2)电子的比荷为
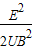 .
.(3)电子打到荧光屏上的位置O点的距离为
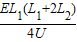 .
.点评:本题是电场加速、偏转及速度选择器的组合.按程序法进行分析研究,偏转问题,运用运动的分解处理,电子离开电场后也运用分解法研究.

练习册系列答案
相关题目
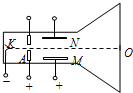 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.

 如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.
如图所示为一种测量电子比荷仪器的原理图,其中阴K释放电子,阳A是一个中心开孔的圆形金属板,AK间加一定的电压.在阳极右侧有一对平行正对带电金属MN,板间存在方向竖直向上的匀强电场O点为荧光屏的正中央位置,K与O的连线M、N板间的中心线重合.电子从阴极逸出并AK间的电场加速后从小孔射出,KO连线方向射M、N两极板间.已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计,在下列过程中,电子均可打到荧光屏上.