��Ŀ����
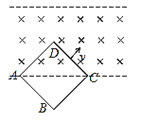
����Ŀ����ͼ��ʾ���㹻���ˮƽ�⻬Բ̨��������һ���⻬�ĸˣ�ԭ��ΪL���ᵯ�����ڸ��ϣ�������Ϊm��A��B��C����С�����������ͨ���⻬�������ӣ���˳�ҲΪL��A��������ֱ���ϡ��ֽ�A����ڵ����϶ˣ���ϵͳ���ھ�ֹ״̬ʱ���������ֱ����н�����37������֪�������ٶ�Ϊg������ʼ���ڵ������ڣ�sin37����0.6��cos37����0.8��
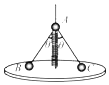
(1)����˶�B��������F�͵��ɵľ���ϵ��k��
(2)��B��C������ͬ�Ľ��ٶ�����ֱ������ת������ת���Ľ��ٶ�Ϊ��0��δ֪��ʱ��B��C���Ҫ����Բ̨�����������ֱ����н���0�����Һͽ��ٶ���0��
(3)������ֱ��£��A����������Բ̨L�ߴ���ֹ���ܵ�С�Ŷ���A�������˶���ͬʱB��C���������෴������Բ̨����ֱ������A��B��C��ʼ����ͬһ��ֱƽ���ڣ��۲A���½���������Ϊ0.4L��A���˶�����͵�ʱ���ٶȴ�СΪa0�����ʱ���ɵĵ�������Ep�Լ�B����ٶȵĴ�Сa��
���𰸡���1��F��0 ![]() ��2��
��2��![]() ��3��0.4mgL��
��3��0.4mgL��![]()
��������
��1��ƽ̨�⻬����B����������֪��˶�B��������F��0
���ɵ��α�������L��L��Lcos��
��A��k��L��mg
��ã�![]()
��2��B��C������������ABCϵͳ����ֱ�������Ϊ�㣬��k��L��Lcos��0����3mg
��ã�![]()
��B����������ʽ�У�mgtan��0��m��02Lsin��0
��ã�![]()
��3����A���½�h��0.4Lʱ��ABC�ٶȾ�Ϊ�㣬�ɻ�е�غ��У�Ep��mgh��0.4mgL
��˴�ʱ����ΪT��������ֱ����н�Ϊ��1����![]()
A�ļ��ٶ���ֱ���ϣ���ţ���˶������У�kh��2Tcos��1��mg��ma0
ͬ����B�У�Tsin��1��ma
��ã�![]()