Question

（选做题，选修3-5）
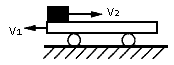
质量为m_B=2 kg的平板车B上表面水平，开始时静止在光滑水平面上，在平板车左端静止着一块质量为m_A=2 kg的物体A，一颗质量为m₀=0.01 kg的子弹以v₀=600 m/s的水平初速度瞬间射穿A后，速度变为v=100 m/s，已知A、B之间的动摩擦因数不为零，且A与B最终达到相对静止。求：
(1)物体A的最大速度v_A；
(2)平板车B的最大速度v_B。

Answer 1

解：
①子弹穿过物体A的过程中，对子弹和物块A，由动量守恒定律得： m₀v₀=m₀v+m_Av_A
解得：v₄=2.5m/s；
②对物块A和平板车B，由动量守恒定律得： m_Av_A=（m_A+m_B）v_B
解得：v_B=1.25m/s。