题目内容
3.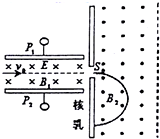 如图所示,速度相同的一束粒子由左端垂直射入质谱仪后的运动轨迹,则下列相关说法中正确的是( )
如图所示,速度相同的一束粒子由左端垂直射入质谱仪后的运动轨迹,则下列相关说法中正确的是( )| A. | 该束带电粒子带正电 | |
| B. | 能通过狭缝S0的带电粒子的速率等于$\frac{E}{{B}_{2}}$ | |
| C. | 若增大入射速度,粒子在磁场中轨迹半圆将变大 | |
| D. | 若保持B2不变,粒子打在胶片上的位置越远离狭缝S0,粒子的比荷越大 |
分析 由图可知,粒子进入匀强磁场B2中受到洛伦兹力而做匀速圆周运动,根据粒子向下偏转,即可知粒子所受的洛伦兹力方向向下,由左手定则可判断粒子的电性;
粒子速度选择器中受到电场力和洛伦兹力两个作用,电场力不变,速度方向不变,可知洛伦兹力与电场力应平衡,由平衡条件即可确定能通过狭缝S0的带电粒子的速率;
粒子进入匀强磁场B2中受到洛伦兹力而做匀速圆周运动,由牛顿第二定律得到半径表达式,明确越远离狭缝S0半径越大,则可求得粒子的比荷的大小.
解答 解:A、由图可知,带电粒子进入匀强磁场B2时向下偏转,所以粒子所受的洛伦兹力方向向下,根据左手定则判断得知该束粒子带正电.故A正确.
B、在平行金属板中受到电场力和洛伦兹力两个作用而做匀速直线运动,qE=qvB1,所以:v=$\frac{E}{{B}_{1}}$,故能通过狭缝S0的带电粒子的速率等于$\frac{E}{{B}_{1}}$.故B错误;
C、粒子在平行金属板中受到电场力和洛伦兹力两个作用而做匀速直线运动,qE=qvB1,若增大入射速度,粒子受到的洛伦兹力大于电场力,则粒子在速度选择器中将向上偏转,不能通过狭缝S0.故C错误
D、粒子进入匀强磁场B2中受到洛伦兹力而做匀速圆周运动,由牛顿第二定律得:
qvB2=m$\frac{{v}^{2}}{r}$,
得:r=$\frac{mv}{q{B}_{2}}$
可见,由于v是一定的,B2不变,半径r越大,则$\frac{q}{m}$越小.故D错误;
故选:A
点评 本题关键要理解速度选择器的原理:电场力与洛伦兹力,粒子的速度一定.粒子在磁场中偏转时,由洛伦兹力提供向心力,由牛顿第二定律则可得到半径.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.质量为100kg的小船以3m/s的速度自西向东行使,船上还有两个质量皆为50kg的运动员相对船静止,忽略阻力.现在,若运动员甲首先沿水平方向以4m/s(相对于静止水面)的速度向东跃入水中,然后运动员乙沿水平方向以同一速率向西(相对静止水面)跳入水中.则二人跳出后小船的速度为( )
| A. | 向东3m/s | B. | 等于0 | C. | 向东6m/s | D. | 1.5m/s |
11.下列说法错误的是( )
| A. | 随着温度的升高,一方面各种波长的辐射强度都会增加;另一方面辐射强度的极大值向波长较短的方向移动 | |
| B. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变短 | |
| C. | 根据海森伯提出的不确定性关系可知,不可能同时准确地测定微观粒子的位置和动量 | |
| D. | 物质波和光波都是概率波 |
18.关于电磁波的应用,下列说法正确的是( )
| A. | 夜视仪利用了红光成像技术 | |
| B. | 利用紫外线的荧光效应来做防伪标识 | |
| C. | 可以利用X射线进行通信、广播 | |
| D. | 医院利用红外线的热效应杀菌消毒 |
 如图所示,把A、B两个完全相同的小球分别用长度均为l=0.10m的绝缘细线连接,悬挂于O点,使小球带上等量正电荷.A、B小球平衡时距离为d=0.12m.已测得每个小球质量是1.2×10-3kg,带电小球可视为点电荷,重力加速度g=10m/s2,静电力常量K=9.0×109 N•m2/C2
如图所示,把A、B两个完全相同的小球分别用长度均为l=0.10m的绝缘细线连接,悬挂于O点,使小球带上等量正电荷.A、B小球平衡时距离为d=0.12m.已测得每个小球质量是1.2×10-3kg,带电小球可视为点电荷,重力加速度g=10m/s2,静电力常量K=9.0×109 N•m2/C2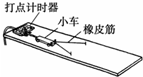 在“探究功与速度变化的关系”实验中.
在“探究功与速度变化的关系”实验中. 在描绘小电珠的伏安特性曲线实验中:
在描绘小电珠的伏安特性曲线实验中: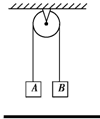 如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过光滑定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.方法如下:
如图所示,两个质量各为m1和m2的小物块A和B,分别系在一条跨过光滑定滑轮的软绳两端,已知m1>m2,现要利用此装置验证机械能守恒定律.方法如下: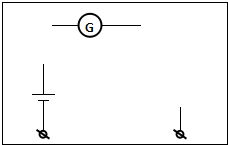 现有一满偏电流为500μA、内阻为1.0×103Ω的电流表
现有一满偏电流为500μA、内阻为1.0×103Ω的电流表 ,某同学想把它改装成中值电阻为500Ω的欧姆表,实验室提供如下器材:
,某同学想把它改装成中值电阻为500Ω的欧姆表,实验室提供如下器材: 的内阻较大,该同学先把电流表
的内阻较大,该同学先把电流表 改装成量程为0~3.0mA的电流表
改装成量程为0~3.0mA的电流表 ,则电流表
,则电流表 应并(填“串”或“并”)联一个电阻箱,将该电阻箱的阻值调为200Ω.
应并(填“串”或“并”)联一个电阻箱,将该电阻箱的阻值调为200Ω. 改装成欧姆表,请选择适当的器材在方框内把改装后的电路图补画完整(含电流表的改装),并标注所选电阻箱和滑动变阻器的符号.
改装成欧姆表,请选择适当的器材在方框内把改装后的电路图补画完整(含电流表的改装),并标注所选电阻箱和滑动变阻器的符号. 的示数为200μA,则该电阻的阻值为750Ω;通过该电阻的电流为1.2mA.
的示数为200μA,则该电阻的阻值为750Ω;通过该电阻的电流为1.2mA.