题目内容
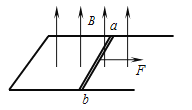
【题目】一块长木板abc长为2L，沿与水平面成θ角倾斜放置，它的ab部分表面光滑，bc部分表面粗糙，两部分长度相等．木板下端口处有一与木板垂直的挡板，挡板上固定一段劲度系数为k的轻弹簧，弹簧长度为0.5L．将一质量为m的物块在木板的顶端c由静止释放，物块将沿木板下滑，已知重力加速度大小为g，下列表述正确的是
A．物块最终会在ab之间某一段范围内做往复运动
B．物块运动过程中克服摩擦力做的功最多为mgLsinθ
C．物块每一次下滑过程达到最大速度的位置是不一样的
D．物块每一次下滑过程中弹簧具有的弹性势能的最大值都等于
【答案】AB
【解析】
试题分析：物块从c到最低点的运动中，物块的势能转化为摩擦生热和弹簧的势能，从最低点返回后弹性势能转化为摩擦生热和物块的重力势能，物块会在木板上做往返运动，每次经过bc面都有能量损失，直至最后的弹性势能只能转化为物块到达b点的重力势能，物块只在ab之间某一段范围内做往复运动，故A正确；物块最后在b与a上方某点之间做往复运动，物块到达最低点时，由mgsinθ=kx，解得：
，
根据能量守恒定律，mg（2L-
）sinθ=Wf+mg（L-）sinθ，解得：Wf=mgLsinθ，故B正确；
物块开始会在b点上方某点和最低点运动，最后在b点和最低点之间运动，故在b点上方某点和最低点运动，每次有能量损耗，故每一次下滑过程达到最大速度的位置是不一样的，但在b点和最低点之间运动，无能量损耗，物块每一次下滑过程达到最大速度的位置是一样的，故C错误；物块第一次到达最低点时，由mgsinθ=kx，解得：x=，根据能量守恒定律得：mgsinθ[2L(
L)]=EP+Q，整理得：EP+Q=mgsinθ（
），故物块第一次下滑过程中弹簧具有的弹性势能的最大值都小于mgsinθ（），故D错误；故选：AB
