题目内容
5.已知地球自传周期为T,半径为R,地球表面重力加速度g,写出同步卫星距离地面高度h和运动速度的表达式?分析 在地球表面万有引力等于重力,同步卫星处万有引力提供同步卫星圆周运动的向心力,据此分析即可.
解答 解:根据题意,在地球表面重力和万有引力相等,即:G$\frac{mM}{{R}^{2}}$=mg
由此可得:GM=gR2
令同步卫星的距地面的高度为h,则由万有引力提供同步卫星的向心力有:
G$\frac{mM}{(R+h)^{2}}$=m(R+h)$\frac{4{π}^{2}}{{T}^{2}}$
代入GM得:$\frac{g{R}^{2}}{(R+h)^{2}}$=(R+h)$\frac{4{π}^{2}}{{T}^{2}}$
整理得:h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R
根据v=$\frac{2π(R+h)}{T}$=$\root{3}{\frac{2πg{R}^{2}}{T}}$
答:同步卫星距地面的高度$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R,运动速度$\root{3}{\frac{2πg{R}^{2}}{T}}$.
点评 地球表面重力和万有引力相等、卫星圆周运动的向心力由万有引力提供这是解决万有引力问题的两大关键突破口.

练习册系列答案
相关题目
16. 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
 如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )
如图所示,矩形线圈的匝数为N,面积为S,内阻为r,绕OO′轴以角速度ω做匀速转动.在它从如图所示的位置转过90°的过程中,下列说法正确的是( )| A. | 通过电阻的电荷量为$\frac{NBSπ}{{2\sqrt{2}(R+r)}}$ | B. | 通过电阻的电荷量为$\frac{2NBS}{R+r}$ | ||
| C. | 外力所做的功为$\frac{{{N^2}{B^2}{S^2}ω}}{N(R+r)}$ | D. | 外力所做的功为$\frac{{π{N^2}{B^2}{S^2}ω}}{4(R+r)}$ |
10.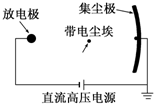 如图为静电除尘器除尘机理的示意图.尘埃在电场中通过某种机制带电,在电场力的作用下向集尘极迁移并沉积,以达到除尘目的.下列表述正确的是( )
如图为静电除尘器除尘机理的示意图.尘埃在电场中通过某种机制带电,在电场力的作用下向集尘极迁移并沉积,以达到除尘目的.下列表述正确的是( )
 如图为静电除尘器除尘机理的示意图.尘埃在电场中通过某种机制带电,在电场力的作用下向集尘极迁移并沉积,以达到除尘目的.下列表述正确的是( )
如图为静电除尘器除尘机理的示意图.尘埃在电场中通过某种机制带电,在电场力的作用下向集尘极迁移并沉积,以达到除尘目的.下列表述正确的是( )| A. | 到达集尘极的尘埃带正电荷 | |
| B. | 电场方向由集尘极指向放电极 | |
| C. | 带电尘埃所受电场力的方向与电场方向相同 | |
| D. | 同一位置带电荷量越多的尘埃所受电场力越小 |
14.某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2,5s内物体的( )
| A. | 路程为65m | B. | 位移大小为25m,方向向上 | ||
| C. | 速度改变量为10m/s,方向向下 | D. | 平均速度为25m/s,方向向上 |
15.一带正电的粒子,重力不计,以初速度vo垂直射向水平地面,此时该粒子在地磁作用下将( )
| A. | 向东偏转 | B. | 向西偏转 | C. | 向南偏转 | D. | 向北偏转 |